It has been very quiet here for a while. That is partly because there is a topic that I wanted to discuss here and since my take was going to be at least somewhat problematic, I felt for a while that I needed to do more reading to get the facts right. But now the time has come for me to talk about: Probabilistic decompression models.
The idea as such is very simple: Many models for decompression including the ones that I talk a lot about in this blog, Bühlmann, VPM-B and also DCIEM are “deterministic” models: They give you a plan and if you stick to it (or dive more conservatively) you should be fine but you must not violate the ceilings they predict at any given time. On the other hand, there are probabilistic models that aim to compute a probability of getting DCS for any possible profile and which you can then turn around and prescribe a maximal probability of DCS and then you optimise your profile (typically for the shortest ascent time) that gives you that prescribed probability of DCS.
That sounds like a great advantage: Don’t we all know that there is no black and white in decompression but there are large grey areas. Even when you stick to the ceilings of your deterministic model there is a chance that you get bent while on the other hand you do not immediately die when you stick your head above the ceiling, quite the opposite, there are chances that even with substantial violation of the decompression plan you will still be fine. That sounds pretty probabilistic to me.
Of course, things are more complicated. Also the deterministic models do not really aim at a black/white distinction. Rather, they are also intended to be probabilistic but with a fixed prescribed probability built in. For recreational diving (here as usually including technical diving but not commercial diving), the accepted rate of DCS is usually assumed to be one hit in a few thousand dives. That seems to be the sweet spot between not too often having to call the helicopter (and most recreational divers never experiencing a DCS hit) and being overly conservative (too short NDL times, too long decompression stops). So, the only difference is that for the probabilistic models, this probability is an adjustable parameter.
You can turn this around: Why would you be interested in dive profiles that have vastly different probabilities of DCS that this conventional one in a few thousand? After all, even for one possible value of p(DCS) it is very hard to collect enough empirical data to pin down the parameters of a decompression model. Why on earth would you want to do that also for probabilities that you do not intend to encounter in your actual diving? Why would I be interested in computing an ascent plan that will bend me one dive in twenty for example? Or in only one dive in a million? That sounds to be overly complicated for useless information.
The answer is exactly in your restricted ability to conduct millions of supervised test dives: Let us assume you have a probabilistic model with a number of parameters that still need to be determined empirically. But you have a priori knowledge that the general form of your model is correct (we will come back to this assumption below), you can do your test dives with depths, bottom times and ascents that your model gives you DCS probabilities in in the range of 5-50% say, depending on the parameters. Much more aggressive than you intend to dive in the end. But such test dives will give you a lot of DCS cases and you do not need too many dives to determine if the true probability is 5%, 20% or 50% and adjust the model parameters accordingly. You gain already a lot of information with just 10-20 dives while for dives with the 1/10000 rate of DCS you need many more dives to have enough DCS cases to establish the true probability.
Once you have established the parameters of your model with these high risk dives where you have to use your chamber a lot to treat your guinea pig divers after bending them you can then use your model for dives that have a much healthier conservatism where your model gives you for example p(DCS)=1/10000.
An example of doing your study in a regime where you expect to bend many contestants is the famous NEDU deep stop study where the divers were in quite cold water with insufficient thermal protection and in which they had to work out on ergometers while in the water all to drive up the expected number DCS cases (there not necessarily with a probabilistic model in the background but just the intend to see a difference in deeper vs shallower decompression schedules where of course 0 DCS cases for both ascents wouldn’t be very informative).
But as so often, there is no such thing as free lunch: You are extrapolating data! You make experiments in a high risk regime of your data and then hope that the same model with the same parameters also in a low risk regime. You are extrapolating your data over several orders of magnitude of probability. This can only work if you can be sure your model is correct in its form and the only thing to determine empirically are the few parameters. But in the real world, in particular in decompression science, such a priori knowledge is not at hand.
Let me illustrate this in a simplified example: Let’s assume, there is only one parameter x and your model is that the logarithm of p(DCS) is a straight line (an affine function) of x
\(\log(p_{DCS}) = m x +b\)Then, in your experiments you do a number of test dives at various values of x, find the corresponding rates of DCS and finally fit the slope m and the intercept b by linear regression.
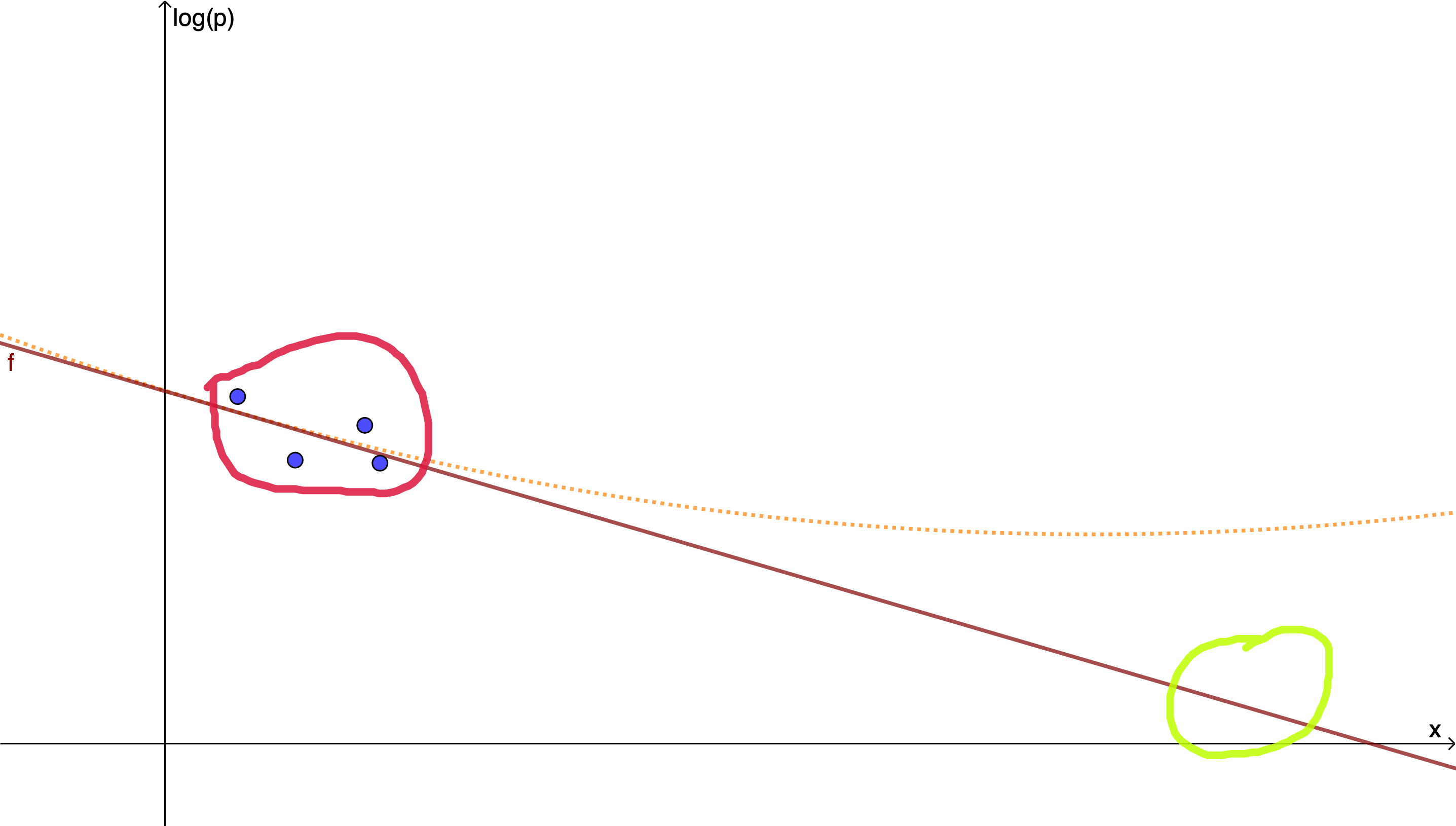
If however the a priori assumption of the model that a straight line does the job is not justified because there is also a small quadratic contribution, say, you can fit your parameters as closely as you want but still get very far off in the extrapolation to where you intend to use your model.
This is of course only an example and for more complicated models you will use a maximum likelihood method to find optimal values of your model parameters given the outcomes of various test dives. But what this will never be able to do is to verify the form of your model assumptions. You are always only optimising the model parameters but never the model itself. For that you need independent knowledge and let’s hope you have that.
VVAL18
To be specific, let us look at one probabilistic algorithm more concretely: VVAL18 which was developed by Edward Deforest Thalmann for the US Navy based on a database of a few thousand navy dives. For military divers, the accepted risk of DCS is much higher, if 2% of the dives result in symptoms that need to be treated that is still considered fine given that decompression chambers are typically available at the dive spot. This model is also known as the Thalmann algorithm and is described for example in short in this technical report. (Similar things could for example be said about the SAUL decompression model which is similar in spirit and also inspired by the navi data)

This model also uses compartments with half times but leaves open the possibility that the partial pressures do not follow the usual diffusive dynamics with the rate of change proportional to the pressure difference to the surroundings but for off-gassing also allow for the possibility of a constant rate (which leads to linear rather than exponential time dependence).
For each compartment i, there is a fixed threshold pressure pth that as an excess pressure is considered harmless and above that a relative excess pressure is calculated
\(e_i = \frac{p_i-p_{amb}-p_{thi}}{p_{amb}}\)To compute the risk, for each second of the dive and each compartment, risk of not getting bent in the second is assumed to be
\(e^{-a_ie_i}\qquad (*)\)for some constants ai. Finally, all these individual risks are considered to be independent, so the “survival probability”, the probability of not developing DCS is assumed to be simply the product of all the individual probabilities for compartments and seconds (since they are in the exponent, you can there integrate the ei over time and sum over tissues).
These constitute the a priori assumptions of the model that I was talking about: The exponential dependence of risk on relative overpressure (*) and the statistical independence of tissues and instances of time. According to these assumptions, your risk of DCS increases exponentially in time when you do longer decompression (assuming the excess pressure is kept constant) for deeper dives or longer bottom times (this is clearly at odds with the assumptions of for example the Bühlmann model that allows you to have arbitrary long decompression obligations as long as you do not violate a ceiling) and you are allowed to have arbitrary large excess pressures if you keep the duration of the excess short enough (tell that to your soda bottle).
With these assumptions, for which I could not find any justification in the literature for, except “we came up with them”, lack of imagination, then the parameters of the model are optimised using maximum likelihood. In the Thalmann case, there three tissues and the parameters to be fitted are the half-times, the thresholds pth and the constants ai.
The three half-times Thalmann ends up with are roughly one minute, one hour and ten hours (with large uncertainties), the thresholds are essentially 0, and the ai are in the 1/50000 range (you can find the values in an appendix of the report cited above, note that time units of minutes are used rather than the hypothetical second I used here).
I have serious doubts about the intrinsic assumptions of (*) and the statistical independence of time segments. But for Navi use where you accept DCS risks of a few percent those may be ok since any model with sufficiently many fitted parameters will reproduce dives with similar parameters. But failed assumptions will bite you when you extrapolate your model out from the high risk regime to recreational diving as failed model assumptions tend to blow up under extrapolation.
I want to mention that I am grateful to the LMU Statistics Lab that I could discuss with them some of the issues mentioned. Of course all mistakes here are my own.