Tag: gradient factors

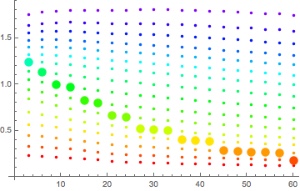
David Doolette has written a blog post “GRADIENT FACTORS IN A POST-DEEP STOPS WORLD” on the GUE blog that has caught some attention on the inter webs. He summarises the state of affairs about the current sentiment against too excessive deep stops, a trend that got momentum in the wake of the NEDU study.

It’s a nice summary but for those who followed the debates about this there are not too many news except in the last paragraph where he describes his personal take away: He says that newer results indicate that the increase in allowed over-pressures with depth (in the Bühlmann model expressed by the fact that the b-parameters are smaller than one and thus the M-value grows faster than the ambient pressure) is doubtful and that in fact the algorithms used by the Navy have the allowed over-pressure independent of depth, i.e. an effective b=1 for all compartments.

As with standard dive computers you are not at liberty to change the a and b parameters of your deco model. Rather the tuneable parameters are usually the gradient factors. So he proposes to set

\(GFlow = b GFhigh\)

citing 0.83 being an average b parameter amongst tissues and thus justifying his personal choice of gradient factors to be 70/85 saying “Although the algebra is not exact, this roughly counteracts the slope of the “b” values.”

This caught my attention as many divers lack a good motivation for some specific setting of their gradient factors (besides quoting that “they always felt good with these settings” and thus ignoring that this is as best subjective anecdotal evidence for a statement the would need a much higher number of tests under controlled circumstances to have any significance.

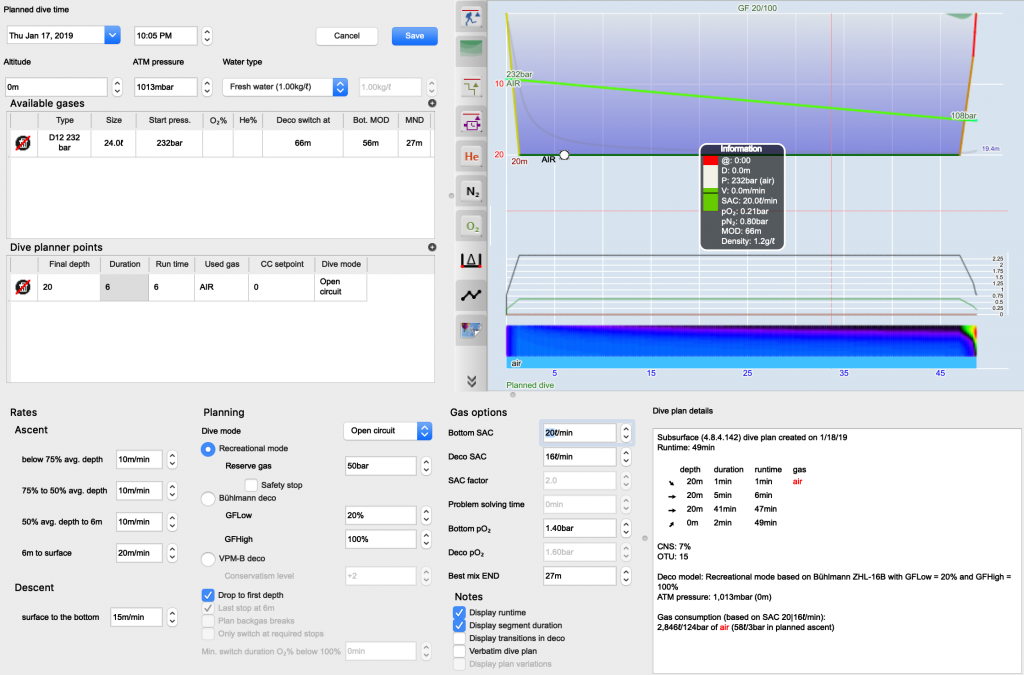
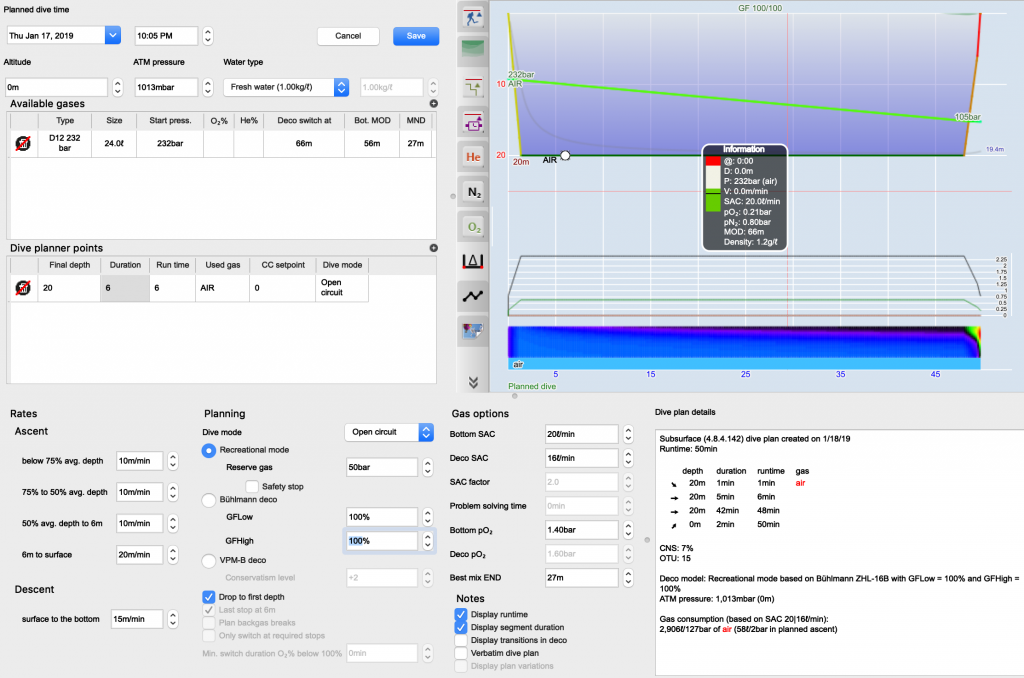
We could add this as a feature to Subsurface where you could turn on “Doolette’s rule” and then your GFlow would automatically be set as 0.83 of your GFhigh (we could even use the actual b value for the compartment and make the GFlow depend on the compartment). Of course, since we have access to the source code, we could directly set the all the b’s to 1 by hand and get rid of the gradient factors in that mode entirely. That might involve also modifying the a’s (as the now depth independent M-value) which made me worry that I might be pulling numbers out of thin air which when implemented might cause other divers to actually use them in their diving while being without any empirical testing, something I wouldn’t like to be responsible for.

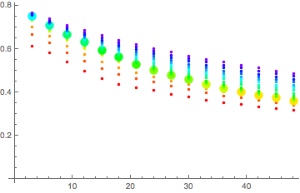
So, rather being the theoretical diver, I fired off mathematica to better understand the “non-exact algebra” and to see if it could be improved. Turns out “non-exact” is somewhat of a euphemism.

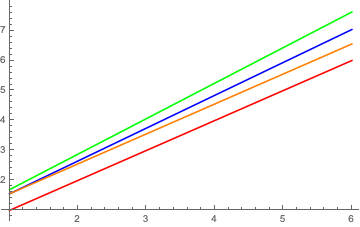
Of course, how bad this approximation is depends on the depth at which GFlow applies (i.e. the first stop depth) but from the plot it is clear that a constant M-value corresponds to smaller and smaller GFlow (as a fraction between the red and green line).

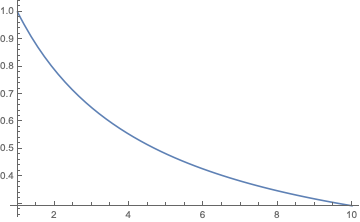
As you can see, for somewhat greater fist stop depths (corresponding to deeper and/or longer dives), to keep a depth independent M-value one needs such a small GFlow that I would consider this to be very well in deep stop territory, opposed to what the blog post started out with.

If you want to play around with the numbers yourself, here is the mathematica notebook.

In my posts here at the theoretical diver, I usually assume that besides some mathematics and physics literacy (which allows me to use formulas) my readers already know about the workings at least of the Bühlmann model and its generalisation using gradient factors.

Of course, that assumption is not always justified and for some time I wanted to write a foundational post on these topics (maybe with some personal twist, let’s see) but I never got around doing that. There is my old text (in German) but that covers only the very basics and in particular it is very short on gradient factors.

Some consolation was that there are a number of such descriptions available on the inter-webs. But now, on the occasion of the Boot trade show, there is a new one written by Ralph Lembcke und Matthias Heinrichs of Heinrichs Weikamp, the manufacturer of OSTC dive computers (and friends of the blog), Matthias and Ralph are now the principal developers of the OSTC firmware. It has a broader audience (and is in German as well) in mind and thus does a good job using diagrams instead of formulas. I like it a lot and give a strong reading recommendation (even though I might phrase the justification for using smaller GFlow differently, and there is of course my private pet peeve of not thinking of tissue half times as part of the model)!

Update September 2020: Now also available in English.

There is an interesting discussion over at ScubaBoard how the non-decompression limit (NDL) is affected by the settings for gradient factors (GFlow and GFhigh), in particular which of the two is relevant. My initial reaction was: It’s clearly GFlow, as that sets the depth of the first stop and the criterion for NDL is that the (theoretical) first stop is at a depth of 0.

Others argued that it must be GFhigh as that applies, by definition, at the surface.

And indeed, in this limit (of the first stop is at the surface) the idea of gradient factors degenerates: In that limit, the rate of change of effective gradient factor as a function of depth diverges. So, like in the last post, there is an interesting point that involves taking limits.

What I had in mind is the implementation in Subsurface: As you can see, as long as there has not been a stop yet (because the ceiling is still above the surface), the effective gradient factor is GFlow. So, in a no decompression dive, you would think, you never see anything else.

But to show that in the recreational mode in the planner turned out so be quite hard: I had to play a lot with the parameters to find a dive where GFlow has any influence on the total dive time of a recreational dive (defined as a dive without mandatory stops and without running out of gas). Eventually I found one: For an air dive to 20m (with an ascent rate of 20m/min for the last segment, see below why this is important), you get a maximal run time of 49min with GF settings 20/100 while you can stay for 50min with GF settings of 100/100. But changing GFhigh has much stronger influence:

What did I miss? In the end, it’s the fine-print of the definition of “first stop depth” that I already talked about in an earlier post: The problem is that for real world dives there is no clear distinction between ascent and stop. So you need to come up with some definition which depth one wants to use to actually anchor GFlow. Subsurface uses the lowest ceiling encountered during the dive so far. But in particular for dives with very little (or none at all) deco obligation that is not exactly what others might consider the first stop depth. The difference is that the diver first need to get to that depth of the ceiling before the ceiling actually becomes a stop depth. And during that ascent, there is already off-gassing going on which can eliminate the ceiling during the time it takes the diver to get there.

As an example, you could have a first ceiling (which as I explained above is determined by GFlow) at say 1m of depth. But then, in this last meter of water, the effective gradient factor has to vary from GFlow to GFhigh. Given that we are talking about dives that are only marginally deco dives, it is likely that this first ceiling comes form a very fast tissue so it is likely that much of it goes away during the short time of ascent to that depth. Then, to find the NDL, the remaining question is if there is ceiling left below the surface. But then the GFlow is already anchored at 1m so for the surface it’s really GFhigh (and GFlow is no longer relevant as there is no ceiling left at 1m where it applies).

So the challenge to find a dive where GFlow makes any difference at all for the NDL was to produce a dive where there is something left of the initial ceiling at the time when the diver gets there in the marginal case of staying a little bit shorter not occurring any stops at all. So the dive must not be too deep (otherwise the ascent takes too long and there is a lot of on the way off-gassing). That’s why I had to increase the ascent rate.

So the upshot is: It is almost entirely GFhigh that sets the difference between a non-stop dive and a decompression stop dive. But if you stay a little bit longer the depth of your first stop (and also the duration) depends a lot on GFlow.

I should not end without pointing out that once more this discussion is quite academic: Gradient factors were invented for dives that have significant deco obligation to force deeper stops. Here, we are in the limit of recreational no-stop diving. So we are really not in the realm of gradient factors. And this manifests itself in the degeneracy of the model in the case of the ceiling being exactly at the surface that determines the NDL. But it was interesting anyway.