Tag: Bühlmann

N2 vs. He, what’s the difference?

 

 

Recently, a blog post on the Shearwater blog was pointed out to me (thanks Jan) that reports on a paper by David Doolette  etal and the Navy Experimental Diving Unit comparing the same 200ft dive with 40min bottom time both on a CCR rebreather once with  trimix 12/44 as diluent and once with 12/88 (i.e. heliox) as diluent. Divers followed a deco plan computed for trimix and the traditional wisdom would have been that a fraction of the heliox divers would get bent thanks to an increased amount of helium in their body. But the study found that this is not the case and only some of the test divers breathing trimix were getting bent.

The NEDU trimix dive replaced with Subsurface.

Here is the dive replanned in Subsurface. One would need gradient factors 110/36 (low/high, note the order!) to come up with this plan, but ok, fine. Notice the unusual pattern on the heat-map.

The upshot apparently is that traditionally one was overestimating the penalty for using lots of helium in short bounce dives (from the perspective of the navy). Helium atoms being much smaller than nitrogen molecules are believed to diffuse much faster into the body and thus prompting deeper stops.

Obviously, this cannot be the whole argument since faster diffusion would also lead to faster desaturation, so here is a post to look a bit deeper into the differences between nitrogen, helium and trimix from the deco perspective. Since this is easiest to understand in its consequences, let us discuss these matters from the perspective of the good old Bühlmann model.

I think it is indeed not controversial that smaller particles diffuse faster but that alone should make zero difference! This might sound surprising but let’s look at Bühlmann’s list of half-times (these are essentially inverses of the diffusion constants). Those are for nitrogen (in minutes):

const double buehlmann_N2_t_halflife[] = { 5.0, 8.0, 12.5, 18.5, 27.0, 38.3, 54.3, 77.0, 109.0, 146.0, 187.0, 239.0, 305.0, 390.0, 498.0, 635.0 };

const double buehlmann_He_t_halflife[] = { 1.88, 3.02, 4.72, 6.99, 10.21, 14.48, 20.53, 29.11, 41.20, 55.19, 70.69, 90.34, 115.29, 147.42, 188.24, 240.03 };

Obviously, there is a difference. But how did he measure those? The answer is: He didn’t. You can come up with those (starting from N2) only by theoretical reasoning. You assume that the relevant physics is diffusion. And that has only one parameter, the diffusion constant or half-time. And that you don’t know a priori. But you can imagine that you only need to look at processes at time scales compared to those encountered during a dive. And there, pressure changes at the order of a few minutes and the total dive length which is a few hours. So anything in between will be relevant. And this is what gives you those numbers! They vary from five minutes to 10.5 hours. Ideally you want to cover the whole range of in-between numbers but of course you can do this only for a finite number of values (here taken to be 16) which you then evenly spread in the interval. Where evenly means that consecutive ones differ by the same percentage (rather than absolute value), i.e. they form a geometric progression. And, guess what, they do.

Obviously, there is a bit of arbitrariness in this procedure, in particular in picking the smallest and the largest value and in the number of intermediate steps. But as long as the slowest or fastest compartment are not the leading compartment for a larger part of the deco and the gaps between adjacent tissue half-times are not too big, those choices should not really matter.

But this means that what seems to be the biggest difference between nitrogen and helium, the difference in half-times is really no difference at all! It only means, we parametrize the range of possible diffusion constants differently. Yes, compartment number four has a different half-time for N2 (18.5min) than for  He (7min) but there are compartments six and seven (half-times 14.48min and 20.53min) which would cover the same time range. (Note that thanks to the diffusion equation, the tissue loading after time is the Laplace transform of the ambient pressure and according to the structural similarity between Laplace and Fourier transform, the half-time plays the role of a frequency, so a tissue gets particularly excited if the ambient pressure changes at the same time scale which is like exciting on oscillator with its resonant frequency).

Keep in mind that “the tissue” does not really correspond to a certain part of the human body like muscles being modeled by compartment x and bones by compartment y (even though some layman’s explanations make you believe that), rather the range of tissues models the range of diffusion constants and our ignorance about the time constants that might play a role in a complex system like that of a diver during the dive.

So, if you did one dive in which the breathing mix contained a given fraction of nitrogen, then the tissue loading of compartment four would be the same as if the same profile would be dived with breathing a mix that contains that fraction now in helium and then in compartment six or seven (ignoring the fact that before the dive, at the surface you were breathing air and not heliox 79).

So much for tissue loadings (where the difference between N2 and He is only in a shift in compartment number). But what about M-values (parametrized by a- and b-coefficients in Bühlmann’s model)? Those are different for He and N2.

Yes, they are. When indexed by compartment numbers. But we just saw, those don’t mean much, we should rather look at them as a function of half-time. And then the difference is much smaller as can be seen by these diagrams:

Orange is helium, blue is nitrogen. There seems to be a systematic difference for slow tissues for a and for fast tissues for b but this goes essentially away once one plots the tolerated ambient pressure (the “M-value”) as a function of tissue loadin according to the linear equation

\(p_{tol}=(p_{i} – a) \times b\)
M-values for He and N2 as a function of tissue pressure and half-time

 

This plot shows \(p_{tol}\) as a function of (the log) of the half-time and the tissue loading and one sees there is hardly any difference between the orange and the blue surface (here is a version that you can rotate to look at it from all sides without coordinate frame though, thanks Mathematica). I computed all these plots in a Mathematica notebook that you can download here.

Again, the upshot is that once you align the tissue half-times, the difference between the two inert gases is quite small. So, why is there a “penalty” for using more helium in your mix (while there above mentioned study finds evidence for not so much difference)? Where does it come into the model?

The answer is that when actually diving trimix, that is having both N2 and He in your mix, one has to combine the effects of the two. In the Bühlmann model, you are supposed to add the partial tissue pressures and use the weighted average (weighted by the fractions of the two inert gases) of the M-values. And here it is, where you combine them using tissue number (and not as I did above) by half-time. The justification would be that due to the different diffusion rates this is what happens in a single tissue in the body (with the above mentioned caveat that these tissues are theoretical constructs of an interpolation and not necessarily reflect real physiological tissues).

The effect is that now some nitrogen load is compared to an M-value which partly comes from He which gives you a much stricter M-value (as the He-M-values are smaller when you compare them with aligned compartment number rather than half-time). This is where the penalty comes from.

To me it sounds as if it is this combining of the gases is actually the part of the Bühlmann model with the weakest justification from a physics point of view. And my interpretation of the NEDU study is that it supports doubts that this is the right thing to do.

It seems, further studies about this part, where one simply takes two gas compartments which happen to have the same compartment number (which is only a coordinate in diffusion constant space after all) and throws them together for the two different gases, are needed. At least, this is where I would put my money that this is an area where the models could be improved (or at least better empirically justified).

 

Update: In a previous version I had claimed that David Doolette had invented the heat-map display of decompression. It was pointed out to me that this was in fact user “UWSojourner” on several fora.

Why is Bühlmann not like Bühlmann

I often see complaints that two different dive planning programs or dive computers do not give identical deco schedules even though both claim to implement the same decompression model. Like both being Bühlmann with gradient factors. Once you implement a model, it should deterministically give you a plan for the ascend.

And yes, in an ideal world that would be true. But in ours, the model does not exist. Even though some description of how one is supposed to compute stops is written down, there are still a lot of undefined details that are up to the implementation to decide (often enough not consciously since the ill-definedness might be rather subtle). And I am not talking about random fudge factors that programmers add to their implementations to make the schedules more conservative and to reduce the DCS risk to divers following the program or computer’s advice (like always increasing the depth by a constant amount or some percentage or letting time run faster upon tissue loading and slower during off-gassing, OSTC I am looking at you!). IN particular, for dive computers with proprietary software the customer will never know which tweaks were implemented (or even advertised as features like taking temperature or heart rate into account or breathing rate or punishing ceiling violations). I am not saying these are bad ideas, it just makes schedules hard to compare

Here, I want to discuss more subtle issues, issues that arise since models are only defined in prose and that is up to interpretation. Like the original Bühlmann model being described in his book and gradient factors essentially defined in a figure on the last page of Erik Baker’s paper. In this respect, VPM-B is different: There exist texts but I find those confusing to say the least (which was also my motivation for some previous posts) and those are silent about things like repetitive diving or how to apply the model to real logged dives rather than in planning. The actual definition of VPM-B is, however, in the original FORTRAN program. And that has deterministic output. So that is clearly defined. On the other hand, the program does not tell you about the reasoning behind it so provides no basis for extrapolation (to things like logged dives).

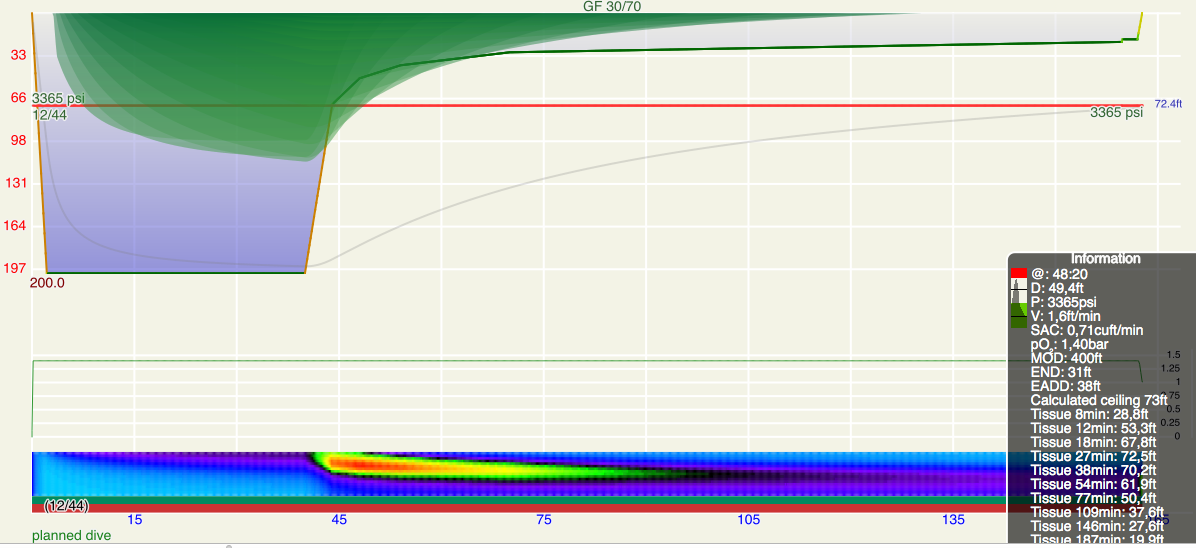
  • When is it time to leave a stop? All models I know provide you with a current minimal ambient pressure given the tissue loadings and the current ambient pressure. So, should you leave your stop once that minimal ambient pressure is less or equal than the ambient pressure of your next potential stop? This might be the naive guess. But one could also take into account not the current ambient pressure but that of the stop. And for gradient factors (see below), one has to take the gradient factor into account not at the current depth but at the depth of the next stop (or ceiling). I have seen implementations that got the maths of this wrong. But there is another thing that one could take into account: There is further off-gassing during the ascend to the next stop. So, the criterium should not be if the next stop is below the ceiling once i leave the previous stop but once I reach the next. To me, this is the only sensible criterium, so Subsurface does this for Bühlmann where it is not specified. But in order to be 100% compatible with the original implementation of VPM-B, using that model, we take the criterium to be the ceiling at the time of leaving the previous stop. The difference is minimal but can make stops one minute shorter or longer (and due to on-gassing on the deeper stops also influence the length of the shallower stops).
  • The next difference is in what actually constitutes stop times: Everybody wants there stops to have integer minute lengths. But what exactly is the length of a stop (which is then subject to integer rounding), starting at the time you leave the previous stop or only at the time you arrive at the next? For 9m/min ascent rate and 3m intervals, this difference is 20s. This is only a rounding effect, so the immediate difference is only one minute per stop. But again, due to on-gassing of slow tissues on deeper stops this difference can multiply at the shallower stops.
  • Looking at the graphics that is supposed to define gradient factors, Gradient factor definition one understands that the GFlow is supposed to be applied at the first stop depth. So far, so good. But what is that exactly? Is the the ceiling at the end of the bottom time? Or the deepest ceiling ever encountered during the dive? Or should we take into account the off-gassing during the ascend and take it to be the first time we actually hit the ceiling (since the first ceiling we see at the end of the bottom time might have moved up during the ascent? The last option is probably what was implied by Baker. And that might well apply to a planned dive. But not so much for a real dive: Image a carful diver that always does his stops one meter too deep (at the price of potentially longer stops). He never reaches the “first stop” in a strict sense because he always stays shy of reaching that stop and waits for it to clear before the further ascent (one could summarize his behavior also in terms of a very very slow ascent rate). So, in  a strict sense, for this diver, GFlow never applies (or only at the surface). Of course, this does not really make sense and thus, to avoid this paradox, in Subsurface we use the deepest ceiling encountered during the dive as the anchor depth for GFlow (also since for logged dives there is no clear distinction between the bottom part of the dive and the ascent).
  • Finally, there are some other smaller ill-defined bits, like in how to average things when diving with different gases (as initially N2 and He are treated separately), how to take care of the notorious water vapor (and which partial pressure assume for it).

So in summery, even if two implementations follow the letters of the definition of a decompression model, they might come up with different deco plans. For all practical purposes, those differences should be small (like a few percent of total decompression time) and thus be hidden in the much larger systematic error of all these very simple models (after all, we do not have good information about all the things that are going on in a diver’s body) but they can be big enough to make people worry since they think decompression is an exact science or even that computer programs should be deterministic. Yes, programs can be deterministic, but it is well possible that a model described only in prose has several different implementations.

 

PS: Something completely different: I set up a Facebook page for this blog. Subscribe it if you want to be notified whenever a new post appears!