This is the second instalment in a series of posts that are inspired by my reading about the SAUL deco model. Paradoxically, I want to report on something that I realised while reading the articles about that model even though Saul Goldmann, SAUL’s inventor, kindof comes to the opposite conclusion.
For the Bühlmann model, I have argued before that the different tissue half times are not really parameters of the model: If you have a tissue in contact with an environment (be it breathing gas or blood) it is pretty natural that gas diffuses between the environment and the tissue with a rate that is proportional to the difference of partial pressures
\(\dot p_i = d_i (p_a – p_i)\).
Here pi is the partial pressure in tissue number i, pa is the ambient partial pressure and di is the diffusion constant (essentially ln(2) divided by the half-time) of that tissue. This is the differential equation that governs all on- and off-gassing of tissues. To complete the Bühlmann model, one only has to specify a maximal tissue partial pressure in relation to the ambient pressure (or better a minimal ambient total pressure for a given tissue partial pressure) for which Bühlmann assumes an affine relation, i.e.
\(p_a \ge b_i (p_i – a_i).\)It is important that the coefficients ai and bi for the tissue number i are really parameters of the model that need to be determined empirically (and for which there are tables). The diffusion constants (and thus tissue half-times), however, are not.
You only need to make sure you satisfy the inequality for all possible tissues, that is for all possible half-times. To do so, you try to do the calculation for all relevant time scales. In the case of (non-saturation) diving, the relevant times go from a few minutes (the shortest relevant time scale of ascents and descents) to a few hours.
Of course, you cannot calculate for all possible times. But you make sure, you cover this range of times with many representative times. And a little further thought reveals that you should spread those representative times geometrically (so also the range of diffusion constants is covered geometrically).
To sum up, you need to know the a’s and the b’s but for the d’s, you essentially cover all possible values. It is important, that for this result we had to know nothing about actual tissues like bones, nerves, muscles or whatever of the human body, since all that is relevant that they have some diffusion constant in the relevant range.
So far, this was all old news.
Today, I want to look at the question, why we can get away with treating all these tissues independently. Why does tissue number i only exchange inert gas with the blood stream or the breathing gas and not with all the other tissues?
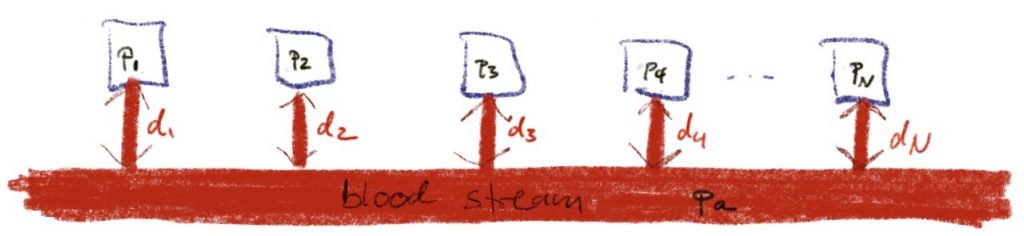
Maybe, this assumption is unrealistic and we should better consider a model that looks like this:
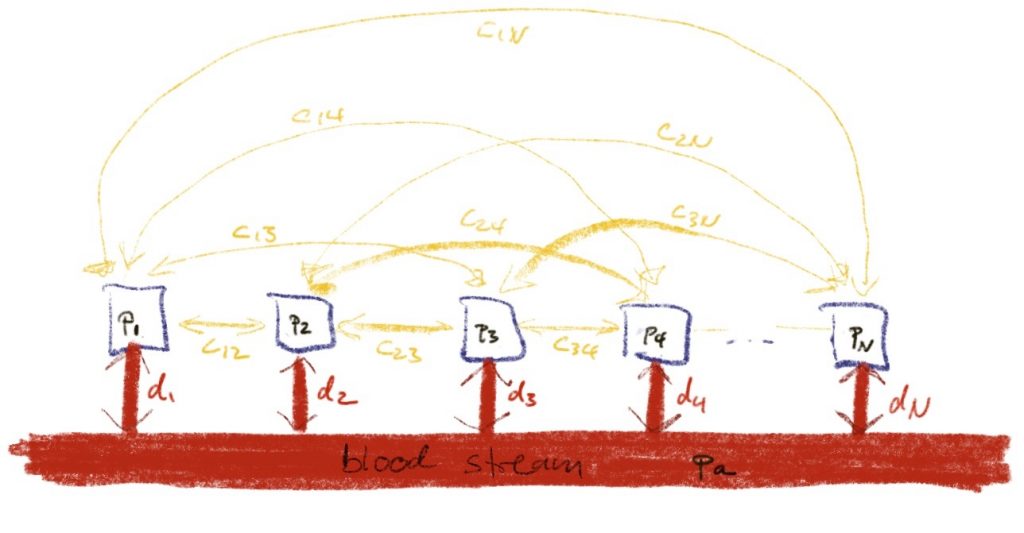
Maybe, we should allow tissues i and j to exchange gas directly. This would be described by a new diffusion constant cij (non-negative and possibly zero if the tissues are not connected) and the new differential equation would look like
\(\dot p_i = d_i (p_a – p_i)+\sum_{j\ne i} c_{ij}(p_j – p_i)\).
In order for no gas to get lost, we would need cij to equal cji. To simplify this, we could assemble the different partial pressure pi into a vector p, the diffusion constants di into a vector d and the new diffusion constants cij into a symmetric matrix C.
If you have only a little experience with ODE’s, you realise that this equation is a linear inhomogeneous ODE and can be written in the form
\(\dot p = Ap + p_a d\)where the matrix A has components
\(a_{ij} = -c_{ij} + \sum_k c_{ik} \delta_{ij} – \delta_{ij} d_i.\)A quick inspection shows that A is symmetric and negative definite (if all di are positive).
The key observation is that we can diagonalise A as
\(A= U^{-1}DU\)where D is diagonal with all negative eigenvalues. Then the above differential equation reads
\({d\over dt}(Up) = D (Up) + p_a Ud.\)But thanks to D being diagonal, we can view this as a new vector Up of tissue partial pressures that obey the original Bühlmann differential equation! So up to taking linear combinations, the Bühlmann model already covers the case of tissues directly exchanging inert gases. Allowing for this apparent generalisation of the model can be converted by simply a change of basis.
So, if we say, that the modelled tissues are not really corresponding to actual tissues (as we already did above) but allow the interpretation that they might be linear combinations of actual tissues, then the Bühlmann model already covers (as long as we cover all possible diffusion constants which we do) the case of inter-tissue gas exchange. It is not a special case in this wider class of modes with interconnected tissues but it is already the generic case.
Let me close with a consistency check: At content depth, pa is constant. In this case, Up converges saturates to
\((Up)_i \to \frac{(Ud)_i}{\lambda_i}p_a.\)or in matrix notation
\(p\to U^{-1}D^{-1}Ud p_a = A^{-1}dp_a.\)But a quick calculation shows that if v is the vector that has ones in all components
\(Av = d\)and thus finally
\(p_i\to A^{-1}dp_a = vp_a\)and hence indeed all tissue partial pressures approach the ambient partial pressure.

Sounds like the magic of models with extra parameters: they will fit anything