N2 vs. He, what’s the difference?

 

 

Recently, a blog post on the Shearwater blog was pointed out to me (thanks Jan) that reports on a paper by David Doolette  etal and the Navy Experimental Diving Unit comparing the same 200ft dive with 40min bottom time both on a CCR rebreather once with  trimix 12/44 as diluent and once with 12/88 (i.e. heliox) as diluent. Divers followed a deco plan computed for trimix and the traditional wisdom would have been that a fraction of the heliox divers would get bent thanks to an increased amount of helium in their body. But the study found that this is not the case and only some of the test divers breathing trimix were getting bent.

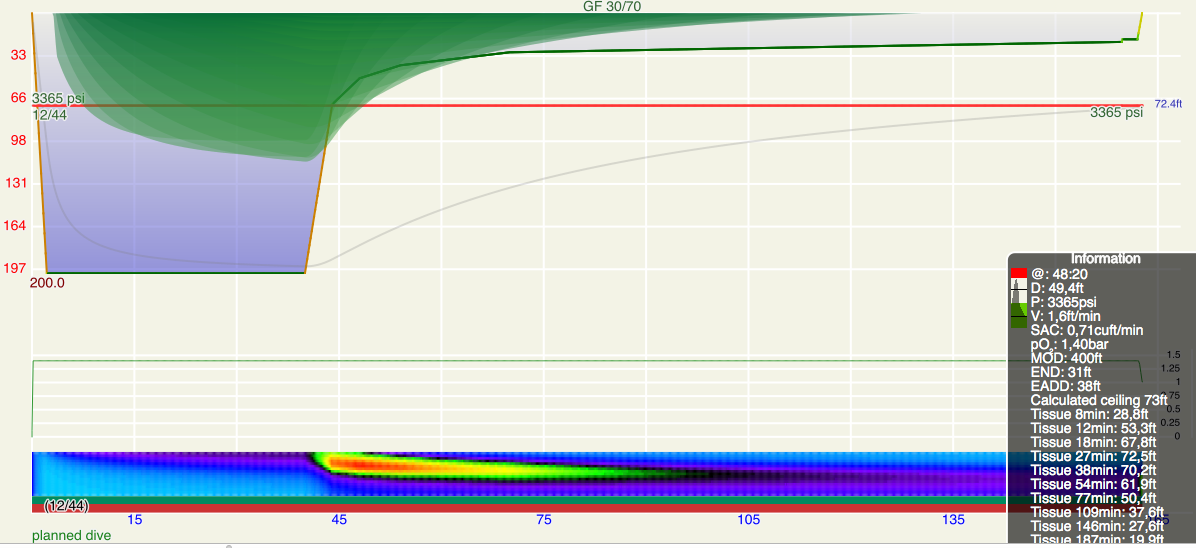
Here is the dive replanned in Subsurface. One would need gradient factors 110/36 (low/high, note the order!) to come up with this plan, but ok, fine. Notice the unusual pattern on the heat-map.

The upshot apparently is that traditionally one was overestimating the penalty for using lots of helium in short bounce dives (from the perspective of the navy). Helium atoms being much smaller than nitrogen molecules are believed to diffuse much faster into the body and thus prompting deeper stops.

Obviously, this cannot be the whole argument since faster diffusion would also lead to faster desaturation, so here is a post to look a bit deeper into the differences between nitrogen, helium and trimix from the deco perspective. Since this is easiest to understand in its consequences, let us discuss these matters from the perspective of the good old Bühlmann model.

I think it is indeed not controversial that smaller particles diffuse faster but that alone should make zero difference! This might sound surprising but let’s look at Bühlmann’s list of half-times (these are essentially inverses of the diffusion constants). Those are for nitrogen (in minutes):

const double buehlmann_N2_t_halflife[] = { 5.0, 8.0, 12.5, 18.5, 27.0, 38.3, 54.3, 77.0, 109.0, 146.0, 187.0, 239.0, 305.0, 390.0, 498.0, 635.0 };

const double buehlmann_He_t_halflife[] = { 1.88, 3.02, 4.72, 6.99, 10.21, 14.48, 20.53, 29.11, 41.20, 55.19, 70.69, 90.34, 115.29, 147.42, 188.24, 240.03 };

Obviously, there is a difference. But how did he measure those? The answer is: He didn’t. You can come up with those (starting from N2) only by theoretical reasoning. You assume that the relevant physics is diffusion. And that has only one parameter, the diffusion constant or half-time. And that you don’t know a priori. But you can imagine that you only need to look at processes at time scales compared to those encountered during a dive. And there, pressure changes at the order of a few minutes and the total dive length which is a few hours. So anything in between will be relevant. And this is what gives you those numbers! They vary from five minutes to 10.5 hours. Ideally you want to cover the whole range of in-between numbers but of course you can do this only for a finite number of values (here taken to be 16) which you then evenly spread in the interval. Where evenly means that consecutive ones differ by the same percentage (rather than absolute value), i.e. they form a geometric progression. And, guess what, they do.

Obviously, there is a bit of arbitrariness in this procedure, in particular in picking the smallest and the largest value and in the number of intermediate steps. But as long as the slowest or fastest compartment are not the leading compartment for a larger part of the deco and the gaps between adjacent tissue half-times are not too big, those choices should not really matter.

But this means that what seems to be the biggest difference between nitrogen and helium, the difference in half-times is really no difference at all! It only means, we parametrize the range of possible diffusion constants differently. Yes, compartment number four has a different half-time for N2 (18.5min) than for  He (7min) but there are compartments six and seven (half-times 14.48min and 20.53min) which would cover the same time range. (Note that thanks to the diffusion equation, the tissue loading after time is the Laplace transform of the ambient pressure and according to the structural similarity between Laplace and Fourier transform, the half-time plays the role of a frequency, so a tissue gets particularly excited if the ambient pressure changes at the same time scale which is like exciting on oscillator with its resonant frequency).

Keep in mind that “the tissue” does not really correspond to a certain part of the human body like muscles being modeled by compartment x and bones by compartment y (even though some layman’s explanations make you believe that), rather the range of tissues models the range of diffusion constants and our ignorance about the time constants that might play a role in a complex system like that of a diver during the dive.

So, if you did one dive in which the breathing mix contained a given fraction of nitrogen, then the tissue loading of compartment four would be the same as if the same profile would be dived with breathing a mix that contains that fraction now in helium and then in compartment six or seven (ignoring the fact that before the dive, at the surface you were breathing air and not heliox 79).

So much for tissue loadings (where the difference between N2 and He is only in a shift in compartment number). But what about M-values (parametrized by a- and b-coefficients in Bühlmann’s model)? Those are different for He and N2.

Yes, they are. When indexed by compartment numbers. But we just saw, those don’t mean much, we should rather look at them as a function of half-time. And then the difference is much smaller as can be seen by these diagrams:

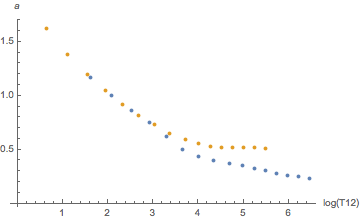
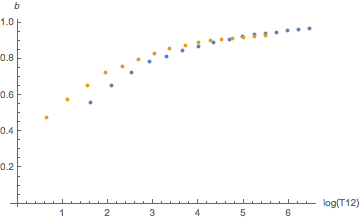
Orange is helium, blue is nitrogen. There seems to be a systematic difference for slow tissues for a and for fast tissues for b but this goes essentially away once one plots the tolerated ambient pressure (the “M-value”) as a function of tissue loadin according to the linear equation

\(p_{tol}=(p_{i} – a) \times b\)

 

This plot shows \(p_{tol}\) as a function of (the log) of the half-time and the tissue loading and one sees there is hardly any difference between the orange and the blue surface (here is a version that you can rotate to look at it from all sides without coordinate frame though, thanks Mathematica). I computed all these plots in a Mathematica notebook that you can download here.

Again, the upshot is that once you align the tissue half-times, the difference between the two inert gases is quite small. So, why is there a “penalty” for using more helium in your mix (while there above mentioned study finds evidence for not so much difference)? Where does it come into the model?

The answer is that when actually diving trimix, that is having both N2 and He in your mix, one has to combine the effects of the two. In the Bühlmann model, you are supposed to add the partial tissue pressures and use the weighted average (weighted by the fractions of the two inert gases) of the M-values. And here it is, where you combine them using tissue number (and not as I did above) by half-time. The justification would be that due to the different diffusion rates this is what happens in a single tissue in the body (with the above mentioned caveat that these tissues are theoretical constructs of an interpolation and not necessarily reflect real physiological tissues).

The effect is that now some nitrogen load is compared to an M-value which partly comes from He which gives you a much stricter M-value (as the He-M-values are smaller when you compare them with aligned compartment number rather than half-time). This is where the penalty comes from.

To me it sounds as if it is this combining of the gases is actually the part of the Bühlmann model with the weakest justification from a physics point of view. And my interpretation of the NEDU study is that it supports doubts that this is the right thing to do.

It seems, further studies about this part, where one simply takes two gas compartments which happen to have the same compartment number (which is only a coordinate in diffusion constant space after all) and throws them together for the two different gases, are needed. At least, this is where I would put my money that this is an area where the models could be improved (or at least better empirically justified).

 

Update: In a previous version I had claimed that David Doolette had invented the heat-map display of decompression. It was pointed out to me that this was in fact user “UWSojourner” on several fora.