Can we calculate no-fly-times?

There are various recommendations how long one should not fly after surfacing from a dive. DAN has recently done a study where they did Doppler measurements on a plane and recommends an interval of 12 hours after a single dive and 24 hours after repetitive diving.

But one would think that it should be possible to use a decompression model that works well under water to compute such a time. So let’s do this in this post or at least compute a conservative estimate. To be specific, we will use the Buhlmann model. We do that calculation compartment by compartment and assume that when leaving the water, the tissue has the maximally allowed partial pressure for surfacing (i.e. this tissue was the guiding tissue for the final part of the ascent). Clearly, this is a conservative assumption. Then, according to the model

\(p_s = (p_i -a)b.\)

Here, ps is the surface pressure and a and b are the usual Bühlmann coefficients.

Then we do a surface interval (whose length we wish to determine in the end) during which the partial pressure decays exponentially:

\(p_i(t) = f_{N_2} p_s+ (p_i(0) – f_{N_2}p_s)e^{-\gamma t}\)

where f is the N2 fraction the the breathing gas (0.79 for air which we are probably breathing while waiting for the plane to board). Finally, we don’t want the cabin pressure to be less than the minimal ambient pressure that Dr. Bühlmann recommends. We want to parametrize the cabin pressure using the barometric formula which asserts (assuming constant temperature) that the pressure drops exponentially at height with decay constant that the pressure is 1/e at about hs=8500m above sea level. So, we set

\(e^{-h/hs} p_s= (p_i(t) -a)b.\)

This we can then solve for t. Actually, being conservative, we want to throw in gradient factors. Again, being conservative, we don’t further linearly extrapolate gradient factors, but will use GFhi everywhere on the surface. Plugging everything in (with the help of Mathematica and some manual massaging) we find

\(e^{\gamma t} = \frac{a GF/p_s + 1-f_{N_2} + GF(1/b -1)}{a GF/p_s – f_{N_2} +e^{-h/h_s}(1+GF(1/b-1))}.\)

Now, we have to plug in numbers. For the cabin pressure, according to Wikipedia, we will assume h=2400m for older aircrafts. The wait times (in hours) for the different compartments are then shown in this plot:

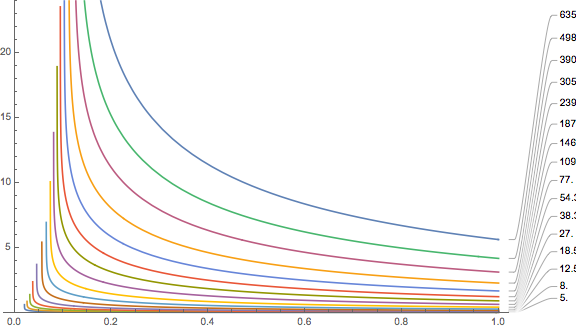
You are supposed to see a number of things:

• The waiting time depends strongly on which tissue we are dealing with. For reasonably large gradient factors, only the tissues with half-times of several hours contribute significant waiting times. Remember, for this calculation, we assumed the loading is at its maximal value when you get out of the water. For realistic sports/tec-diving scenarios (as opposed to saturation diving) that should be quite hard even on a weeklong liveaboard  with at least five dives a day. If slightly faster tissues are leading, the inferred no-fly times are much shorter, probably shorter than the queue at check-in. I looked at some data from real dive trips where people got everything out of their booked liveaboard but they got nowhere close to exciting the slow tissues. In the Subsurface planner I had to do five consecutive 2-hour dives with less than two hour surface interval to see at least some ceiling for the 239 minute compartment. In the plots, this has the blue line and leads to a no-fly time of much less than 5 hours.
• The plot ends on the left (small gradient factors) with diverging values. These divergences move to higher gradient factors when you increase the cabin pressurisation equivalent altitude (for example by assuming a loss of cabin pressure, remember this is when the oxygen masks are supposed to drop from the ceiling)

  

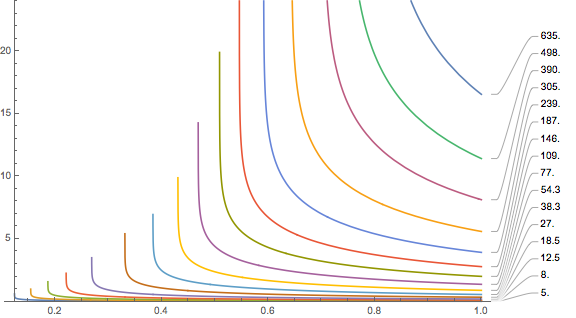
  This comes about as the no-fly time becomes infinite or even complex as according to the Bühlmann-with-gradient-factors limit, your are not allowed to be at the ambient pressure at that altitude even when saturated with the nitrogen that you experience at sea level. We can compute this limiting altitude by solving
  \(f_{N_2} p_s = e^{-h/h_s} p_s (GF/b-GF +1) + a GF /p_s\)
  for the altitude via
  \(e^{-h/h_s} = \frac{f- aGF/p_s}{GF/b -GF +1}.\)
  This is shown here, the maximum altitude after waiting an infinite amount of time: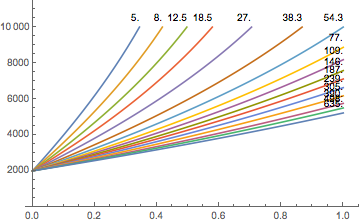

  

   

• All these calculations are for air (or nitrox underwater since all we used was the assumption that the nitrogen saturation is at the limit). In particular, in view of an earlier post (N2 vs. He, what’s the difference?) there should not be large differences.
• You could try to repeat the same argument for VPM-B but according to that model, if you followed it during the ascent, the no fly time would always be infinite: The ascent is determined such that when you surface and stay at ambient pressure, you will just create the maximum amount of free gas that is barely allowed. So going to any altitude and lowering the ambient pressure further would release more free gas than allowed, no matter how long you waited. The only way out would be to produce fewer bubbles on the earlier ascent while still in the water, then you would have some reserves to go to altitude.

What are we supposed to conclude from this? One takeaway message is waiting for the recommended 24 hours is not totally off, in particular if there is a chance that your very slow tissues have loaded a significant amount of nitrogen.

On the other hand, for realistic dives, 24 hours is likely on the very conservative side. At least from the perspective of decompression theory. From this perspective it is a total mystery to my what kind of reasoning dive computers use to determine a no-fly time.

Apart from these model considerations, DCS symptoms often enough do not show up immediately after a dive but up to several hours later. And when you are in that situation that you find yourself with DCS symptoms (even those that would have occurred irrespective of flying or not) your chances for immediate proper treatment are probably much higher if you are not confined to an aircraft above the middle of the ocean. So even from that perspective it makes sense to wait a bit more to make sure you will not need a chamber in the next few hours.

PS: If you want to play around with the formulas, here is my Mathematica notebook.