Tag: Decompression

CCR Schreiner Equation

Since there was a question on Scuba Board about how to compute the tissue pressures when diving a CCR (i.e mainlining constant partial pressure of oxygen) when changing depth at a constant rate. When putting this on a computer I would say doing it for small time steps and pretending to be at constant depth for that short amount of time doesn’t do much wrong and you will end up doing this anyway (at least that’s what we do in Subsurface). But for the fun of it, let’s work out the analytic solution.

Let’s start by figuring out the inert gas ambient pressure at a given depth. We call \(p_d\) the diluent partial pressure, \(p_{O2}\) the partial pressure supplied from the oxygen cylinder (note that this is not the oxygen partial pressure since there is going to be some oxygen in the diluent as well), \(d\) is the depth, \(f_{O2}\) is the fraction of oxygen in the diluent while \(f_i\) is the fraction of the inert gas we are computing in the diluent.

There are two obvious equations: The ambient pressure is equal to the diluent pressure plus the oxygen pressure in the loop:

$$ p_d + p_{O2} = p_a = p_{surf} + dg\rho$$

Here, \(p_{surf}\) is the surface pressure, and \(\rho\) is the density of water and thus \(g\rho\) the conversion factor between depth and pressure. The second equation says that the total partial pressure of oxygen (from diluent and oxygen cylinder combined) has to equal the set point pressure \(p_s\):

$$f_{O2} p_d + p_{O2} = p_s.$$

We can subtract both equations to eliminate \(p_{O2}\) and find

$$ p_d = \frac{p_{surf} + g\rho d -p_s}{1-f_{O2}}.$$

This goes into the usual diffusion equation for the inert gas loading in the tissue \(p_t\) that we are ultimately interested in:

$$\dot p_t = -\gamma( p_t -f_i p_d).$$

\(\gamma\) is the usual diffusion constant that is related to the inverse of the tissue half-time by a factor of \(\ln(2)\). Finally, we want the depth to change linearly in time, so \(d=d_0+vt\) where my sign convention is that \(v\) is the descend velocity, make it negative for ascends.

So we have to solve a linear inhomogeneous ODE with constant coefficients which we could tackle by “varying the constants”, but of course we are lazy and let Mathematica do the job. After a bit of massaging, we find

$$p_t = \frac{f_i}{1-f_{O2}} \left( e^{-\gamma t} -1\right) \left( p_s + \frac{vg\rho}\gamma\right) + e^{-\gamma t}\left( p_0 – \frac{f_i}{1-f_{O2}} (p_{surf} + d_0g\rho)\right) + \frac{f_i}{1-f_{O2}}(p_{surf} + dg\rho)$$

where \(p_0\) is the initial tissue loading. So, here you go this is the CCR Schreiner equation. Or, if you want to follow the tradition to attaching names to simple solutions of ODEs, I allow you to call it the Helling equation.

Update: If you are worried that a constant water vapour pressure has not been taken into account, you can bring it in by replacing the set point by the actual set point plus the water vapour pressure in all equations above.

VPM-B: How to compute your deco

This is the first technical post about the inner workings of the VPM-B deco model. Here I will just present the algorithm (including the relevant formulas, some of them maybe in an unusual form) while the physical motivation or derivation will be the subject of a future post.

I try not to parrot the original explanations (which, honestly, I do not really understand) but rather put in words what I learned by staring long enough at the subsurface implementation of the model. As I explained earlier, we tried to make this an independent implementation but of course in the end we made sure it produces the identical deco schedules to the original FORTRAN code (that we took as the definition of the model).

First of all, it is not that different from the Bühlmann model, it rather builds on it. For the sake of presentation, I will assume you are familiar with how that model works (if not, I wrote a brief summary with some background in German, to be translated to English soon). In particular, it computes the same tissue loadings with inert gases following a simple diffusion equation

$$\frac{dp_i}{dt} = \alpha_i(p_{amb}-p_i)$$

where the time constant \(\alpha_i\) is essentially the inverse tissue half-time.

The only difference is how to compute the current ceiling for a snapshot of tissue loadings (“tensions” in the deco theory speak) \(p_i\): Bühlmann proposes an affine dependence on the ambient pressure (with the affine relation given in terms of the famous \(a\) and \(b\) coefficients. If you use gradient factors, this affine relation is further modified (depending on your lowest ceiling), but when you plot the ceiling as a function of \(p_i\) it is still a straight line, i.e. affine.

This is different for VPM-B: Only in the zero’s approximation it is still a straight line. In fact, there the ceiling is simply given by a maximal gradient (difference between tissue pressure and ambient pressure) that is independent of the depth:

$$p_{amb} – p_i \le G_{0,i}.$$

This is called the initial gradient \(G_0\). In this approximation, VPM-B is like Buehlmann, only with different a and b coefficients.

For the next approximation, the “Boyle compensation” we need to know a little bit about bubbles. in fact, the only thing one needs to know is that they have a surface and in the total energy balance of the bubble the surface contributes proportional to its area:

$$E_{surf}= \gamma r^2$$

for a bubble of radius r (we can absorb all kinds of numerical constants like \(4\pi\) in the proportionality constant \(\gamma\). Then the force on the bubble surface that wants to shrink it is

$$F_{surf} = \frac{\partial E_{surf}}{\partial r} = 2\gamma r.$$

Finally, this force acts on all of the surface, by dividing by its area again, we get the surface’s contribution to the pressure

$$G=\frac{2\gamma}r.$$

This type of formula, the a bubble surface contributing to the bubble’s internal pressure by \(2\gamma/r\) you will see over and over again.

In particular, that the deepest point in the dive, or actually when reaching the first ceiling, the gradient \(G_0\) is exactly this. And the Boyle compensation means that the (now depth dependent) maximal gradient (i.e. ambient pressure minus tissue pressure) is given by letting such a bubble expand according to Boyle’s law, i.e. by assuming that \(pV\) is constant. \(p\) inside the bubble (which is supposedly the same as the tissue pressure) is then given by the ambient pressure plus the momentary maximal gradient while the volume is proportional to \(r^3\) which according to the above formula is proportional to \(1/G^3\). So in total, the allowed difference between the tissue and the ambient pressure at depth \(d\) is given by solving

$$\frac{G+p(d)}{G^3} = \frac {G_0+p_{1st\ ceiling}}{G_0^3}$$

So, rather than being a straight line, the maximal gradient is now the solution of a cubic equation (for which, in Subsurface, we use an analytic expression rather than running a Newton root finder as in the original implementation).

So far, I did not tell you what the initial gradient \(G_0\) is. The VPM-B expression for it is

$$G_0 = 2 \frac\gamma{\gamma_c} \frac {\gamma_c – \gamma}{r_{reg}}.$$

Here, \(r_{reg}\) is the crushing radius which is again determined from an expression of a bubble surface tension:

$$\frac{2(\gamma_c-\gamma)}{r_{reg}} = p_{max} + \frac{2(\gamma_c-\gamma)}{r_{crit}}$$

Here \(\gamma\) and \(\gamma_c\) are some surface tensions (effectively parameters of the model) as is \(r_{crit}\). The latter is where one can tune the conservatism of the model: Each level of conservatism (like three levels in VPM-B+3) increases \(r_{crit}\) by 5 percent. \(p_{max}\) is the maximal ambient pressure encountered during the dive. In principle, it is also assumed that over time, \(r_{reg}\) also exponentially approaches \(r_{crit}\) again, but it is totally safe to ignore this since the decay time is supposed two weeks, far too long to play any role at the typical time scales of the dive.

Now, you have everything to compute a deco schedule: Like in the Buehlmann model, you know for each depth what the maximal gradient is.

Turns out, these schedules take far too long. This is where the “critical volume algorithm” comes into play. We now slightly increase the first gradient (the role so far played by \(G_0\)) which then is also subject to the Boyle compensation.

The idea here is that the body can tolerate an additional amount of gas going into bubbles. The maximal volume, again, is a model parameter and it is compared to the excess volume as follows: One assumes there is some distribution of bubble sizes. By enlarging the gradient \(G_0\) to \(G_0′\), the number of additional bubbles will be (this is one of the places where I do not understand the derivation, but let’s take the expression anyway) proportional to

$$\frac{G_0′-G_0}{G_0′-\alpha G_{crush}}.$$

Here, \(\alpha\) is another constant and \(G_{crush}\) is the maximal excess of the ambient pressure over the tissue pressure over the dive which also happens to be the pressure gradient over the surface of the bubble (if that is too big, we are in the “impermeable regime” and then there is another Boyle type compensation).

Furthermore, rate of additional out gasing is assumed to be proportional to the gradient \(G_0′\) (totally ignoring the first Boyle compensation) and the whole thing lasts (assuming a constant gradient) over all of the decompression time (defined as the time from the first tissue starting to release gas again until we reach the surface). This decompression time \(t_D\) is what we computed above where I said we can now compute a deco plan from the gradients.

Once we reach the surface, there is still an overpressure in the tissue compared to the ambient pressure, it starts with \(G_0′\) (again ignoring the Boyle compensation) and then, according to the diffusion equation above, approaches 0 exponentially. so the time integral of the gradient yields \(G_0’/\alpha_i\). Throwing all together, we get as a criterium for the maximal \(G_0′\)

$$V\ge \frac{G_0′-G_0}{G_0′-\alpha G_{crush}} G_0′ \left(t_D +\frac 1{\alpha_i}\right)$$

This we then solve for \(G_0′\) which we can use for computing a new deco schedule which gives a new \(t_D\) and we repeat this until \(G_0′\) does not change anymore.

Apart from some minor fine print (like how in detail the deco schedules are computed) is all there is to VPM-B. With this information, you should, in principle be able to implement it yourself.

In the next post, I will look into the physics that is invoked to argue for some of the expressions that I only quoted here.

VPM-B: Wie funktioniert’s (deutsche Übersetzung)

Dies ist der erste technische Post darüber, wie VPM-B funktioniert. Ich werde nur den Algorithmus beschrieben (mit allen wichtigen Formeln, einige davon vielleicht  in ungewohnter Form), während die physikalische Herleitung in einem späteren Post behandelt werden wird. 

Ich werde nicht versuchen, die ursprüngliche Herleitung nachzubeten (auch schon alleine, weil ich sie nicht wirklich verstehe), sondern vielmehr beschreiben, was ich durch langes Starren auf unsere Implementierung des Modells in Subsurface gelernt habe. Wie vorher schon erklärt haben wir versucht eine unabhängige Neuimplementierung zu machen, haben aber natürlich sicher gestellt, dass die Austauschpläne des ursprünglichen FORTRAN-Programms reproduziert werden. Dieses haben wir letztendlich als die Definition von VPM-B hergenommen.

Zunächst ist dieses dem Bühlmannmodell sehr ähnlich und baut darauf auf. Für diesen Post nehme ich an, dass dieses bekannt ist (falls nicht habe ich hier mal eine kurze Zusammenfassung aufgeschrieben). Insbesondere werden die Sättigungen der verschiedenen Gewebe mit Inertgasen mit der gleichen einfachen Diffusionsgleichung beschrieben:

$$\frac{dp_i}{dt} = \alpha_i(p_{amb}-p_i)$$

wobei die Zeitkonstante \(\alpha_i\) im wesentlichen der Kehrwert der Halbwertzeit des Gewebes ist. 

Der einzige Unterschied besteht darin, wie die Ceiling (die momentan minimal erlaubte Tiefe) aus den Gewebesaettigungen \(p_i\) berechnet wird: Bühlmann verwendet einen affine Zusammenhang mit dem Umgebungsdruck (die Geradengleichung wird durch die gekannten \(a\) und \(b\) Koeffizienten parametrisiert. Verwendet man Gradientenfaktoren, die wird Geradengleichung noch weiter modifiziert (abhängig von der maximalen Ceiling, aber die Ceiling, geplottet als Funktion von  \(p_i\) bleibt eine Gerade, ist also affin).

Für VPM-B ist dies anders: Nur in der nullten Näherung bleibt es eine Gerade: In der Tat wird die Ceiling einfach durch einen konstanten Gradienten (die Differenz zwischen Umgebungsdruck und Gewebedruck) gegeben, dieser ist sogar von der Tiefe unabhängig:

$$p_{amb} – p_i \le G_{0,i}.$$

Dieser Gradient wird als Anfangsgradient  \(G_0\) bezeichnet. In dieser Näherung verhält sich VPM-B genau wie ein Buehlmannmodell mit modifizierten a und b Koeffizienten.

Für die nächste Näherung, die “Boyle-Kompensation” müssen wir etwas über Blasen wissen. Alles, was wir brauchen, ist, dass diese eine Oberfläche haben und dass die Oberfläche zur Gesamtenergie proportional zu ihrer Fläche beiträgt:

$$E_{surf}= \gamma r^2$$

für eine Blase mit Radius \(r\) (wir können numerische Faktoren wie \(4\pi\) in der Proportionalitätskonstantante \(\gamma\) absorbieren). Die Kraft auf die Oberfläche, die diese zu verkleinern sucht, ist dann

$$F_{surf} = \frac{\partial E_{surf}}{\partial r} = 2\gamma r.$$

Diese Kraft wirkt auf die gesamte Fläche, teilen wir durch den Flächeninhalte erhalten wir einen Beitrag zum Druck in der Blase:

$$G=\frac{2\gamma}r.$$

Derartige Formeln, bei denen eine Blasenoberfläche  \(2\gamma/r\) zum Druck beiträgt, werden im Folgenden immer wieder auftauchen.

Insbesondere zu dem Zeitpunkt im Tauchgang mit der tiefsten Ceiling ist der Gradient \(G_0\) genau dies. “Boyle-Kompensation” bedeutet, dass der von nun an tiefenabhängige Gradient (also der Umgebungsdruck minus Gewebedruck) dadurch gegeben ist, dass man eine Blase nach dem Boyle-Marriott-Gesetz expandieren lässt, also dass man annimmt, dass \(pV\) konstant ist. \(p\) im Inneren der Blase (was nach dem Modell mit dem Gewebedruck gleich ist) wird dann berechnet als der Umgebungsdruck plus dem momentanen maximalen Gradienten. Das Volumen der Blase ist proportional zu \(r^3\) und dies ist nach der obigen Formel proportional zu \(1/G^3\). Alles in allem ist die erlaubte Differenz zwischen Gewebe- und Umgebungsdruck in der Tiefe \(d\) gegeben durch die Lösung von

$$\frac{G+p(d)}{G^3} = \frac {G_0+p_{1st\ ceiling}}{G_0^3}.$$

Folglich ist der der maximale Gradient keine Gerade mehr, sondern die Lösung einer kubischen Gleichung (für die wir in Subsurface auch einen analytischen Ausdruck verwenden statt wie im Originalcode eine Nullstellensuche mittels Newtonverfahren zu veranstalten).

 

Ich habe noch nicht erklärt, wie der Anfangsgradient \(G_0\) berechnet wird. Für VPM-B lautet der Ausdruck dafür

$$G_0 = 2 \frac\gamma{\gamma_c} \frac {\gamma_c – \gamma}{r_{reg}}.$$

Hier ist  \(r_{reg}\) der “Crushing-Radius”, der sich mittels

$$\frac{2(\gamma_c-\gamma)}{r_{reg}} = p_{max} + \frac{2(\gamma_c-\gamma)}{r_{crit}}$$

aus der Oberflächenspannung der Blase berechnen lässt.

Hier wiederum sind  \(\gamma\) und \(\gamma_c\) Oberflächenspannungen (am Ende: Modellparameter), ebenso wie \(r_{crit}\). Letzteres ist der Parameter, an dem man den Konservatismus des Modells einstellen kann: Jede zusätzliche Konservatismusstufe (zum Beispiel VPM-B+3) erhöht \(r_{crit}\) um 5 Prozent.  \(p_{max}\) ist das Maximum des Umgebungsdrucks während des Tauchgangs. Im Prinzip soll man diesen auch wieder exponentiell  an  \(r_{crit}\) angleichen; dies kann man aber getrost ignorieren, da die Halbwertzeit von zwei Wochen viel länger als alle relevanten Zeitskalen eines Tauchgangs sind.

Jetzt haben wir alles, was wir brauchen, um eine Deko-Profil zu berechnen: Für jede Tiefe kennen wir wie im Buhlmann-Modell den maximal erlaubten Überdruck.

Es stellt sich heraus, dass die so erhaltenen Dekoprofile viel zu lange dauern. Hier kommt der “Kritische-Volumen-Algorithmus” ins Spiel. Wir erhöhen leicht den Anfangsgradienten (bisher war das \(G_0\) und unterwerfen den dann ebenso der Boyle-Korrektur.

Die Idee dabei ist, dass der Körper eine bestimmte zusätzliche Menge an Gas in Blasenform verträgt. Dieses erlaubte Volumen ist wiederum ein Modellparameter und wird mit einem wie folgt für einen Anfangsgradienten \(G_0′\) berechnet: Es wird angenommen, dass es vor dem Tauchgang eine bestimmte Verteilung der Blasenzahl abhängig von ihrer Größe im Körper gibt. Dadurch, dass der Anfangsgradient von \(G_0\) auf \(G_0′\) erhöht wird, erhöht sich die Zahl der wachsenden Blasen (generell wachsen grosse Blasen, da bei ihnen der Druckanteil durch die Oberflächenspannung kleiner ist, siehe oben, während kleine schrumpfen). Die Zahl der zusätzlich wachsenden Blasen ist dann in linearer Näherung proportional zu (und dies ist einer der Orte, wo ich die Herleitung nicht verstehe, aber verwenden wir den Ausdruck trotzdem):

$$\frac{G_0′-G_0}{G_0′-\alpha G_{crush}}.$$

 

Hier ist  \(\alpha\) ein weiterer Modellparameter und  \(G_{crush}\) ist der maximale Überdruck des Umgebungsdrucks zum Gewebedruck während des Tauchgangs und nach den Regeln des Modells ebenso der maximale Unterschied zwischen dem Innen- und dem Außendruck einer Blase (wenn dieser zu groß ist, kommen wir ins “nichtpermeable Regime” und man wendet eine weitere Boyle-Kompensation an).

Eine weiter Annahme ist, dass die Rate mit der Gas in die Gasphase in Blasen geht, proportional zum Gradienten \(G_0′\) ist (die erfolgte Boyle-Compensation fällt hier unter den Tisch). Da man also annimmt, dass der Gradient während der Deko (definiert als die Zeit, zwischen dem Zeitpunkt, bei dem das erste Gewebe beginnt, den Gewebedruck wieder abzubauen bis zum Erreichen der Oberfläche) konstant ist, multiplizieren wir den Gradienten mit der Dekozeit (dies ist die Zeit \(t_D\) die wir oben berechnet haben, als wir den Dekoplan aus den Gradienten berechnet haben).

Sobald wir die Oberfläche erreichen, gibt es immer noch einen Überdruck im Gewebe, zunächst \(G_0′\) (wiederum wird die Boyle-Kompensation unterschlagen) und im Folgenden fällt dieser exponentiell entsprechend der obigen Diffusionsgleichung auf 0. Somit ist das Zeit-Integral des Gradienten an der Oberfläche \(G_0’/\alpha_i\). Nimmt man alles zusammen, ist das Kriterium für den neuen Gradienten \(G_0′\)

$$V\ge \frac{G_0′-G_0}{G_0′-\alpha G_{crush}} G_0′ \left(t_D +\frac 1{\alpha_i}\right)$$

Dies löst man nach \(G_0′\) auf, was dann für einen neuen Dekoplan benutzt wird, der wiederum ein neues \(t_D\) ergibt. Dieses Verfahren wiederholt man, bis sich \(G_0′\) nicht mehr ändert.

Bis auf etwas Kleingedrucktes (wie etwa wie der Dekoplan aus dem Gradienten im Detail berechnet wird) ist dies der gesamte VPM-B Algorithmus. Mit diesen Informationen kann man ihn im Prinzip selber implementieren.

In einem zukünftigen Post plane ich dann die Physik anzusehen, die aufgerufen wird, um die hier verwendeten Gleichungen herzuleiten.

VPM-B Gradients as Gradient factors

In a comment, Rick suggested that given that in the end, VPM-B computes depth dependent maximal gradients, one could compare those to the depth dependent gradients computed from the Buehlmann model and expressed as gradient factors (i.e. as percentage of the gradient of a plain vanilla Buehlmann gradient). Here is what I found when I did this.

 

For concreteness, I computed deco schedules with Subsurface for a dive to 120m leaving the bottom at runtime 20min with TMX18/50 (yes, I know this is far too much pO2, but for deco that does not matter), EAN50 and EAN100. For some reason, my ascent speeds are set to 9m/min up to 75% average depth, then 6m/min up to 6m and 1m/min for the final ascent. With Bühlmann with GF 30/80, I obtain a plan that reaches the surface at a runtime of 188min while for VPM-B+1 it takes only 141min.

Actually, I patched subsurface a little bit (see this branch on github) that, during deco, it prints out the allowed gradient for all tissues at all deco stops. This output I ran thru a mathematica notebook  to produce these plots:

 

On the x-axis, we have depth in meters while on the y-axis, we have the current gradient factor. The different colored dots are the different tissues (red being those with the shortest halft-time) with the thick dot indicating the leading tissue, i.e. the tissue that is causing the current stop.

The first diagram is Bühlmann while the second is VPM-B.

A few remarks are in order: First, why is Bühlmann not a single line from GF 30 to GF 40? This is because of the way I compute things: The exact Bühlmann a and b coefficients depend on the gas mixture currently in the tissue. In addition, what is actually computed is the maximal ambient pressure at the ceiling (which is the current depth only for the leading tissue) for that tissue and the gradient I plot is the difference between that and the current ambient pressure. So this is not exactly the right thing for tissues that are not leading. But still we see, it is a nice band of values and they all nicely move between 30% and 80%.

For the VPM-B plot, on the other hand, we see that the variation within a tissue is much less but the gradient factor varies a lot more between tissues. After all, the actual variation in gradient factor with depth comes about mainly because the leading tissue is changing and much less from the cubic curve that implements the Boyle compensation.

The other thing that is striking is the scale: At the last deco stop, the effective gradient factor is 124% for the leading tissue (while for some slower ones it is as high 180% (which never matters as that tissue never leads). In fact, a Bühlmann plan with GF 20/125 leads to a very similar profile.

Here are the actual profiles: First, Bühlmann GF 30/80

Depth

Duration

Runtime

Gas
➘ 120m 7min 7min (18/50)
➙ 120m 13min 20min
➚ 51m 9min 29min
– 51m 2min 31min
➚ 48m 1min 32min
– 48m 1min 32min
➚ 45m 1min 33min
– 45m 2min 34min
➚ 42m 1min 35min
– 42m 2min 36min
➚ 39m 1min 37min
– 39m 4min 40min
➚ 36m 1min 41min
– 36m 3min 43min
➚ 33m 1min 44min
– 33m 4min 47min
➚ 30m 1min 48min
– 30m 6min 53min
➚ 27m 1min 54min
– 27m 6min 59min
➚ 24m 1min 60min
– 24m 10min 69min
➚ 21m 1min 70min
– 21m 5min 74min EAN50
➚ 18m 1min 75min
– 18m 7min 81min
➚ 15m 1min 82min
– 15m 8min 89min
➚ 12m 1min 90min
– 12m 13min 102min
➚ 9m 1min 103min
– 9m 20min 122min
➚ 6m 1min 123min
– 6m 20min 142min EAN100
➚ 3m 3min 145min
– 3m 40min 185min
➚ 0m 3min 188min

Then VPM-B+1: 

Depth

Duration

Runtime

Gas
➘ 120m 7min 7min (18/50)
➙ 120m 13min 20min
➚ 63m 7min 27min
– 63m 1min 28min
➚ 57m 1min 29min
– 57m 1min 30min
➚ 54m 1min 31min
– 54m 1min 31min
➚ 51m 1min 32min
– 51m 2min 33min
➚ 48m 1min 34min
– 48m 1min 34min
➚ 45m 1min 35min
– 45m 2min 36min
➚ 42m 1min 37min
– 42m 2min 38min
➚ 39m 1min 39min
– 39m 3min 41min
➚ 36m 1min 42min
– 36m 3min 44min
➚ 33m 1min 45min
– 33m 3min 47min
➚ 30m 1min 48min
– 30m 4min 51min
➚ 27m 1min 52min
– 27m 5min 56min
➚ 24m 1min 57min
– 24m 7min 63min
➚ 21m 1min 64min
– 21m 4min 67min EAN50
➚ 18m 1min 68min
– 18m 5min 72min
➚ 15m 1min 73min
– 15m 6min 78min
➚ 12m 1min 79min
– 12m 8min 86min
➚ 9m 1min 87min
– 9m 12min 98min
➚ 6m 1min 99min
– 6m 15min 113min EAN100
➚ 3m 3min 116min
– 3m 22min 138min
➚ 0m 3min 141min

Finally Bühlmann 20/125:

Depth

Duration

Runtime

Gas
➘ 120m 7min 7min (18/50)
➙ 120m 13min 20min
➚ 54m 8min 28min
– 54m 1min 29min
➚ 51m 1min 30min
– 51m 2min 31min
➚ 48m 1min 32min
– 48m 1min 32min
➚ 45m 1min 33min
– 45m 2min 34min
➚ 42m 1min 35min
– 42m 2min 36min
➚ 39m 1min 37min
– 39m 2min 38min
➚ 36m 1min 39min
– 36m 3min 41min
➚ 33m 1min 42min
– 33m 3min 44min
➚ 30m 1min 45min
– 30m 5min 49min
➚ 27m 1min 50min
– 27m 5min 54min
➚ 24m 1min 55min
– 24m 6min 60min
➚ 21m 1min 61min
– 21m 4min 64min EAN50
➚ 18m 1min 65min
– 18m 4min 68min
➚ 15m 1min 69min
– 15m 7min 75min
➚ 12m 1min 76min
– 12m 8min 83min
➚ 9m 1min 84min
– 9m 13min 96min
➚ 6m 1min 97min
– 6m 12min 108min EAN100
➚ 3m 3min 111min
– 3m 21min 132min
➚ 0m 3min 135min

Shortening deco by diving deeper

In VPM-B you can shorten your deco by doing another dive before.  Sounds crazy? But this is what this model predicts as I recently learned from Subsurface user who thought he was reporting a bug. To be concrete, let’s plan an air dive to 40m with 30min bottom time (just for concreteness, maybe this is not the optimal gas choice but let’s keep things simple, the argument does not depend on this). With conservatism +2 we get the following plan
<
Runtime: 93min

depth

duration

runtime

gas
➘ 40m 2min 2min air
➙ 40m 28min 30min
– 18m 6min 36min
– 15m 4min 40min
– 12m 6min 46min
– 9m 8min 54min
– 6m 13min 67min
– 3m 23min 90min
➚ 0m 3min 93min

But then add a 60m for 30m dive a bit less than two days (this is the limit that Subsurface considers two dives “repetitive diving”) before and you get:

Subsurface dive plan (surface interval 44:00)
Runtime: 78min

depth

duration

runtime

gas
➘ 40m 2min 2min air
➙ 40m 28min 30min
– 15m 8min 38min
– 12m 5min 43min
– 9m 6min 49min
– 6m 9min 58min
– 3m 17min 75min
➚ 0m 3min 78min

So, you get out of the water 15 minutes earlier! From the point of view of a Bühlmann-type model this sounds totally ridiculous: You would think that the effect of the previous dive is to add inert gas saturation to your tissues and indeed, even for VPM-B that is the case, but the consequences are opposite. The reason is that the previous dive sets the “maximal crushing pressure” and thus the “crushing radius” at the deepest point of the dive. And, as you know from a previous post, this enters the maximal gradient (at least the initial one) that VPM-B will allow you: Translated into gradient factors, without previous dive, Subsurface computes effective GFs as 24/71 versus as a second dive 26/92.

I was even more surprised that in the VPM-B literature this is considered a feature rather than a bug of the model: The previous dive pre-compresses the bubbles and thus they are less dangerous (or something like this). See the very last paragraph of this article.

Actually, to see this behaviour in Subsurface, you cannot use the latest version (or you have to comment out  the lines
for (ci = 0; ci < 16; ci++) {
max_n2_crushing_pressure[ci] = 0.0;
max_he_crushing_pressure[ci] = 0.0;
}

in the function clear_vpmb_state() in deco.c as I did)  as we decided this is too odd and rather opted for the more conservative option to reset the crushing pressure between dives. But that of course poses the question “What is exactly ‘between dives’?”. Is a short visit to the surface starting a second dive and thus magically resetting the state of bubbles in your body?

And of course the underlying question remains (until somebody does an empirical study): Can you really shorten the deco time by pre-compressing the diver?

It doesn’t even have to be a separate dive. According to VPM-B, I can bounce to 60m and immediately return back to 40m and then I get the benefit of shorter deco (compared to the version of the dive where I stayed at 40m):

Runtime: 79min

depth

duration

runtime

gas
➘ 60m 3min 3min air
➚ 40m 2min 5min
➙ 40m 25min 30min
– 15m 8min 38min
– 12m 5min 43min
– 9m 6min 49min
– 6m 10min 59min
– 3m 17min 76min
➚ 0m 3min 79min

Ratio Deco – is it nonsense?

[This is a post by Rick Walsh but this information got lost when this blog moved to a new server.]

When I mentioned to one of my dive buddies I was considering taking a GUE Tech 1 course, his response was “I wouldn’t trust that ratio deco crud”. Another explained calculating ratio deco by: average the depth of your dive; double it; add the last two digits of the serial number of your bottom timer; divide by the number of divers in your team, which is always three; then subtract the number you first started with.

For better or worse, there is a perception among many of us non-DIR (or not yet DIR) decompression divers that ratio deco is dangerous voodoo that should be avoided. But could it be justified?

Let me state now that I have no training in ratio deco, have never used it myself, and I am not advocating its use. If you are interested in applying it to your diving, I encourage you to take a course that covers it and how and when it can be used, and most importantly its limitations. Do not take reading something on the internet as a substitute for appropriate training. This post is intended to discuss the concept of ratio deco far more than the practice. I mention GUE, but the concept applies just as well to other versions of “ratio deco”.

What is Ratio Deco?
Ratio deco is a method for calculating or adjusting a dive decompression profile, which does not require referring to a decompression dive computer, tables or software. As such, the plan can be adjusted or re-calculated on-the-fly during the dive without relying on a dive computer’s decompression calculations.

To many, that sounds too good to be true. Almost all decompression software, dive computers and tables in current use are based on Buhlmann or VPM-B decompression models or some varient thereof. These models have received theoretical and real-life testing, include calculation for sixteen different theoretical tissues, and permit unlimited combinations of dive depths, durations, breathing gasses. Surely this cannot be replaced by a new decompression model calculated on-the-fly by the diver.

In science, engineering, medicine, and many other disciplines, there are countless complicated mathematical models that cannot be generalized by a simple function. However, by controlling some variables, the relationship between others become simplified. It is possible to use linear approximations for non-linear functions over limited ranges with acceptable levels of accuracy.

In reality, ratio deco is not a decompression model. Rather it is a series of approximate relationships and trends that can be observed from ascent schedules calculated using existing models. Searching the internet suggests GUE Ratio Deco is derived from either VPM-B with +2 conservatism, or Buhlmann with approximately 30/85 gradient factors. Either way, it is attempting to replicate a bubble model profile, so comparing it to VPM-B +2 is justifiable.

Whether bubble models generally, or VPM-B specificaly, are the best choice of decompression model is another topic or much debate. But if we think of ratio deco as an approximation of VPM-B used within set limits, the concept is not so radical.

Simplifying a complex model
What variables can be controlled that would permit the simplification of a decompression model?
– Bottom gas
– Decompression gasses
– Ascent and descent rates

GUE and related organizations have adopted standard gas mixes, selected according to dive depth, and have standard ascent and descent rates. With these known, for a set depth and over a limited range in duration, it should be possible to find a linear approximation of the relationship between bottom time and decompression time.

Example profiles
An internet search for “Ratio Deco” brings up a number of hits, including a Team Foxturd blog post. The post gives a procedure for using ratio deco in line with GUE Tech 1 practice. Adopting a bottom gas of either 21/35 or 18/45 trimix, and deco gas of 50% nitrox, the ratio of bottom time to deco time for a 45m dive is given as 1:1. For dives in the 30-48m depth range, the deco time should be adjusted by 5min per 3m depth greater or less than 45m. For example, a 25 minute bottom time at 48m would result in a deco time of 25min (1:1 ratio) + 5min (+3m depth adjustment) = 30min. For a 30min bottom time at 38m, the deco time would be 30min (1:1 ratio) – 10min (-6m depth adjustment) = 20min. GUE Tech 1 limits dives to 30 minutes planned decompression, so implicitly this approximation is applicable within this limit.

Of course, there is more to the decompression profile than the decompression time. Common to both Buhlmann and VPM-B models, a typical ascent profile comprises an initial ascent off the bottom up to the first stop, followed by a series of decompression stops and a final ascent to the surface from the last stop at 3m or 6m. The Team Foxturd blog post divides the ascent into portions:
(a) ascend from the bottom to 80% of the bottom ambient pressure (approximately three quarters of bottom depth) at 9m/min
(b) slow ascent rate to 6m/min to allow “deep stops” to clear while ascending to the gas change and start of “intermediate stops” at 21m
(c) spend the first half the calculated deco time on the “intermediate stops” (the 21m to 9m stops, inclusive), with each stop of approximately equal duration
(d) spend the second half of the calculated deco time at the 6m “shallow stop”
(e) ascend to surface at 1m/min

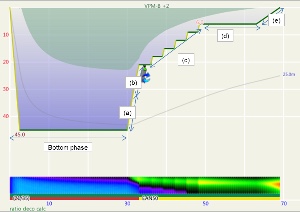
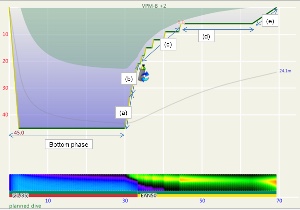
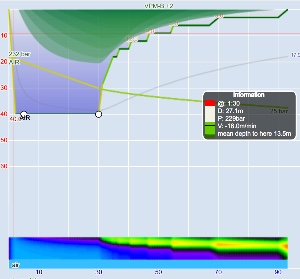
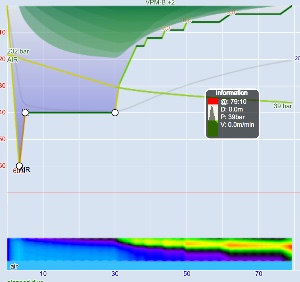
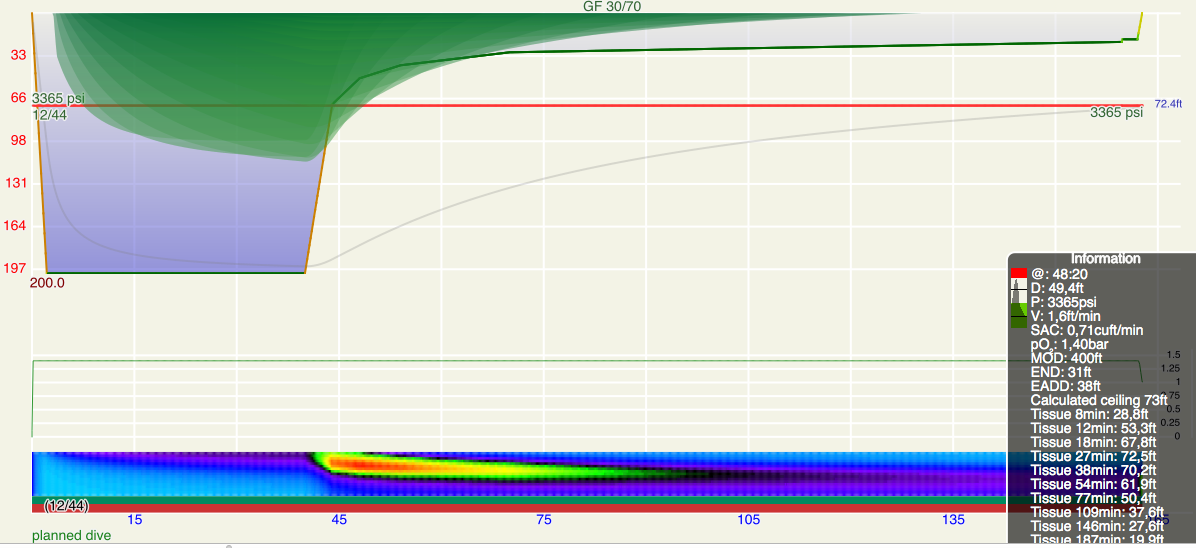
These steps are annotated in Figures 1 and 2. Figure 1 is the profile calculated using Ratio Deco as outlined by Team Foxturd for a 30min bottom time at 45m using 21/35 trimix bottom gas and 50% nitrox deco gas, while Figure 2 is a VPM-B +2 decompression profile calculated in Subsurface for the same bottom time and depth. The VPM-B +2 ceiling is plotted in green in both figures. The Ratio Deco profile spends slightly longer in the “intermediate stops” and slightly less time in the “shallow stop”, but the profiles are quite similar, and importantly the ratio deco profile does not break the ceiling +2. In both instances, the ceiling clears by the end of the 6m stop (end of deco time as defined above), so ascending to the surface over 6 minutes provides an extra buffer.

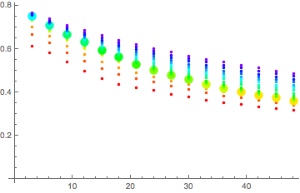
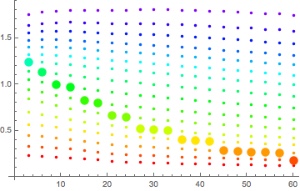
Figures 3 and 4 compare the bottom time to the deco time for VPM-B +2 dives to 45m and 51m, respectively, using 21/35 or 18/45 trimix bottom gas and 50% nitrox decompression gas. As described above, deco time is taken as the time from the first stop until leaving the 6m stop. It does not include the time to ascend from the bottom to the first stop, or the 6 minutes to ascend at 1m/min from the 6m stop to the surface. For comparison, the 1:1 ratio line is plotted on the 45m plot, and the 1:1 ratio plus 10 minutes (5 minutes per 3m increments beyond 45m) line is plotted on the 51m plot. So to is a line at 1:1 (or 1:1 + 10 minutes) ratio plus 6 minutes, representing the surfacing time, which is when the ceiling must have cleared so as not to be broken.

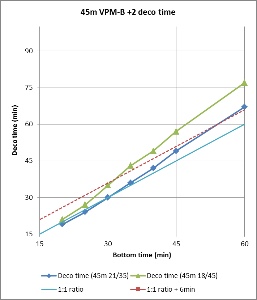
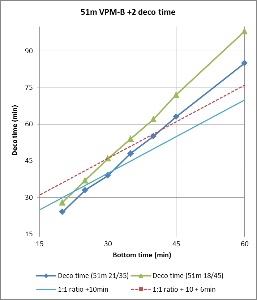
Figure 3 shows that for a 45m dive, the 1:1 bottom time to deco time ratio provides a good approximation when using 21/35 trimix bottom gas, up to about 35 minute bottom time. Beyond this the decompression time increases, diverging away from the 1:1 ratio. However, the 6 minutes taken to surface from the last stop provides some buffer, so for dives using 21/35 trimix, the ratio might be used up to about 50 minute bottom time without breaking the VPM-B +2 ceiling. Compared to 21/35, 18/45 trimix includes a greater portion of inert gas, so it is not surprising that decompression time is increased when using 18/45 trimix bottom gas. But for dives with bottom time up to 30 minutes, the 6 minutes surfacing time provides enough of a buffer that the VPM-B +2 ceiling might not be broken.

Figure 4 shows that for a 51m dive, the 1:1 + 10 minutes bottom time to deco time ratio is a poor fit. To be clear, this is beyond the specified depth range (maximum 48m) in the Team Foxturd post. It is more conservative than VPM-B for shorter bottom times and more aggressive for longer bottom times. However, up to 30 minute bottom time, the 6 minutes surfacing time provides enough of a buffer that the VPM-B +2 ceiling might not be broken when using either 21/35 or 18/45 trimix bottom gas.

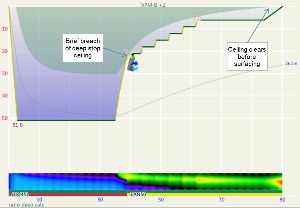
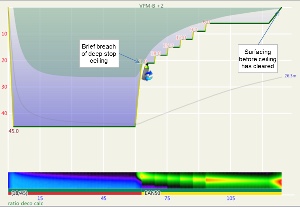
Another way to compare ratio deco ascent schedule to the VPM-B model is to enter the ratio deco profile into Subsurface as a dive and see if the VPM-B +2 ceiling is broken at any point. If the ceiling is not broken, the profile is acceptable according to the model, and if the ceiling is broken the profile does not comply with the model. Where the ceiling is broken is also relevant. Some divers would excuse spending a minute or two just above a deep stop ceiling calculated with a bubble model like VPM-B (which calculate much deeper ceilings early in the ascent than a conventional Buhlmann model), so long as the time was minimal. Such a case is illustrated in Figure 5, which shows a 51m dive with 35 minute bottom time using 18/45 trimix bottom gas and 50% nitrox for decompression. Surfacing before the ceiling had cleared, such as illustrated by Figure 6 for a 45m dive with 60 minute bottom time, would be considered more risky.

Figures 7 and 8 plot the total runtime for profiles calculated using the ratio deco method outlined by Team Foxturd according to bottom time for 45m and 51m dives (noting that 51m exceeds the depth limit given), respectively. Also plotted are the runtimes when the VPM-B +2 ceiling clears, calculated by entering the ratio deco profile into Subsurface. For instances when it took longer than the total dive time for the ceiling to clear, the time to clear was determined by extending the final stop as long as necessary.

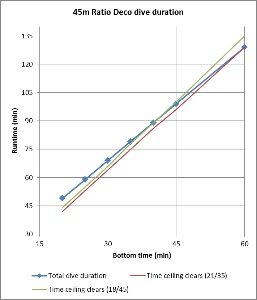
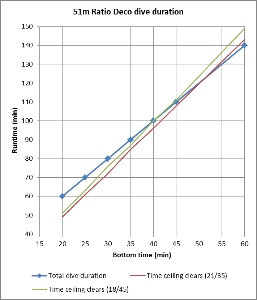
These figures show that for 45m and 51m dives with bottom time up to 35 minutes, the VPM-B +2 ceiling clears before surfacing in accordance with the ratio deco profile, when either 21/35 or 18/45 trimix bottom gas is used. However, brief breaches of the deep stop ceiling occurred when using 18/45 for 30 or 35 minute bottom time. For 40-45 minute bottom time, the ceiling clears just before or just after calculated ratio deco surface time and the deep stop ceiling is also breached. For bottom times exceeding 45 minutes, the ratio becomes increasingly unsatisfactory and risky.

Summary
The above examples demonstrate that it is possible to develop a approximation of a decompression model that provides a reasonable fit over a limited range of depths, bottom times and breathing gasses. Going beyond these limits the approximation starts to fall apart. Undoubtedly there exists, or could be created, approximations that are reasonable for greater depths, longer bottom times, different breathing gasses, altitude diving, and non-square profiles. But with more variations, modifications and adjustments to deal with different situations and contingencies, what started out as a reasonably simple approximation rapidly becomes complicated. Each adjustment introduces its own inaccuracies, not to mention the opportunity for human error.

Understanding trends and the effect of changes to depth, time and gas selection on a decompression model and plan is very powerful. This is the basis for any ratio deco “rules”. Even when the primary means of planning relies on software, and even when a dive computer is used to determine “revisions” to a planned dive, ratio deco can be used as an efficient cross-check. It is very easy to enter an incorrect depth in Subsurface or any other planning software, and it is very easy to select an incorrect gasmix (or neglect to select one at all) when using a dive computer.

Anyone using ratio deco methods for diving needs appropriate training and must understand the limits of the approximation. Not only that, they need to understand the limits of their own ability. This is especially true if they intend to use the technique for on-the-fly planning. Am I really up to calculating my decompression schedule during the dive? Will I have enough gas for the new plan? What about my buddy? How would I deal with lost gas? The ratio deco examples above approximate a VPM-B +2 profile. Many divers and experts disagree on whether VPM-B or Buhlmann (or Thalmann or RGBM) are better models, and many would regard +2 conservatism as not conservative enough.

A little knowledge is a dangerous thing, and this is certainly true of ratio deco. Training in ratio deco should cover not just the principle, and not just a set of rules of thumb, but must also reinforce the limitations of the technique and the need for dive planning to consider more than just developing a decompression schedule.

Why is Bühlmann not like Bühlmann

I often see complaints that two different dive planning programs or dive computers do not give identical deco schedules even though both claim to implement the same decompression model. Like both being Bühlmann with gradient factors. Once you implement a model, it should deterministically give you a plan for the ascend.

And yes, in an ideal world that would be true. But in ours, the model does not exist. Even though some description of how one is supposed to compute stops is written down, there are still a lot of undefined details that are up to the implementation to decide (often enough not consciously since the ill-definedness might be rather subtle). And I am not talking about random fudge factors that programmers add to their implementations to make the schedules more conservative and to reduce the DCS risk to divers following the program or computer’s advice (like always increasing the depth by a constant amount or some percentage or letting time run faster upon tissue loading and slower during off-gassing, OSTC I am looking at you!). IN particular, for dive computers with proprietary software the customer will never know which tweaks were implemented (or even advertised as features like taking temperature or heart rate into account or breathing rate or punishing ceiling violations). I am not saying these are bad ideas, it just makes schedules hard to compare

Here, I want to discuss more subtle issues, issues that arise since models are only defined in prose and that is up to interpretation. Like the original Bühlmann model being described in his book and gradient factors essentially defined in a figure on the last page of Erik Baker’s paper. In this respect, VPM-B is different: There exist texts but I find those confusing to say the least (which was also my motivation for some previous posts) and those are silent about things like repetitive diving or how to apply the model to real logged dives rather than in planning. The actual definition of VPM-B is, however, in the original FORTRAN program. And that has deterministic output. So that is clearly defined. On the other hand, the program does not tell you about the reasoning behind it so provides no basis for extrapolation (to things like logged dives).

  • When is it time to leave a stop? All models I know provide you with a current minimal ambient pressure given the tissue loadings and the current ambient pressure. So, should you leave your stop once that minimal ambient pressure is less or equal than the ambient pressure of your next potential stop? This might be the naive guess. But one could also take into account not the current ambient pressure but that of the stop. And for gradient factors (see below), one has to take the gradient factor into account not at the current depth but at the depth of the next stop (or ceiling). I have seen implementations that got the maths of this wrong. But there is another thing that one could take into account: There is further off-gassing during the ascend to the next stop. So, the criterium should not be if the next stop is below the ceiling once i leave the previous stop but once I reach the next. To me, this is the only sensible criterium, so Subsurface does this for Bühlmann where it is not specified. But in order to be 100% compatible with the original implementation of VPM-B, using that model, we take the criterium to be the ceiling at the time of leaving the previous stop. The difference is minimal but can make stops one minute shorter or longer (and due to on-gassing on the deeper stops also influence the length of the shallower stops).
  • The next difference is in what actually constitutes stop times: Everybody wants there stops to have integer minute lengths. But what exactly is the length of a stop (which is then subject to integer rounding), starting at the time you leave the previous stop or only at the time you arrive at the next? For 9m/min ascent rate and 3m intervals, this difference is 20s. This is only a rounding effect, so the immediate difference is only one minute per stop. But again, due to on-gassing of slow tissues on deeper stops this difference can multiply at the shallower stops.
  • Looking at the graphics that is supposed to define gradient factors, Gradient factor definition one understands that the GFlow is supposed to be applied at the first stop depth. So far, so good. But what is that exactly? Is the the ceiling at the end of the bottom time? Or the deepest ceiling ever encountered during the dive? Or should we take into account the off-gassing during the ascend and take it to be the first time we actually hit the ceiling (since the first ceiling we see at the end of the bottom time might have moved up during the ascent? The last option is probably what was implied by Baker. And that might well apply to a planned dive. But not so much for a real dive: Image a carful diver that always does his stops one meter too deep (at the price of potentially longer stops). He never reaches the “first stop” in a strict sense because he always stays shy of reaching that stop and waits for it to clear before the further ascent (one could summarize his behavior also in terms of a very very slow ascent rate). So, in  a strict sense, for this diver, GFlow never applies (or only at the surface). Of course, this does not really make sense and thus, to avoid this paradox, in Subsurface we use the deepest ceiling encountered during the dive as the anchor depth for GFlow (also since for logged dives there is no clear distinction between the bottom part of the dive and the ascent).
  • Finally, there are some other smaller ill-defined bits, like in how to average things when diving with different gases (as initially N2 and He are treated separately), how to take care of the notorious water vapor (and which partial pressure assume for it).

So in summery, even if two implementations follow the letters of the definition of a decompression model, they might come up with different deco plans. For all practical purposes, those differences should be small (like a few percent of total decompression time) and thus be hidden in the much larger systematic error of all these very simple models (after all, we do not have good information about all the things that are going on in a diver’s body) but they can be big enough to make people worry since they think decompression is an exact science or even that computer programs should be deterministic. Yes, programs can be deterministic, but it is well possible that a model described only in prose has several different implementations.

 

PS: Something completely different: I set up a Facebook page for this blog. Subscribe it if you want to be notified whenever a new post appears!

N2 vs. He, what’s the difference?

 

 

Recently, a blog post on the Shearwater blog was pointed out to me (thanks Jan) that reports on a paper by David Doolette  etal and the Navy Experimental Diving Unit comparing the same 200ft dive with 40min bottom time both on a CCR rebreather once with  trimix 12/44 as diluent and once with 12/88 (i.e. heliox) as diluent. Divers followed a deco plan computed for trimix and the traditional wisdom would have been that a fraction of the heliox divers would get bent thanks to an increased amount of helium in their body. But the study found that this is not the case and only some of the test divers breathing trimix were getting bent.

The NEDU trimix dive replaced with Subsurface.

Here is the dive replanned in Subsurface. One would need gradient factors 110/36 (low/high, note the order!) to come up with this plan, but ok, fine. Notice the unusual pattern on the heat-map.

The upshot apparently is that traditionally one was overestimating the penalty for using lots of helium in short bounce dives (from the perspective of the navy). Helium atoms being much smaller than nitrogen molecules are believed to diffuse much faster into the body and thus prompting deeper stops.

Obviously, this cannot be the whole argument since faster diffusion would also lead to faster desaturation, so here is a post to look a bit deeper into the differences between nitrogen, helium and trimix from the deco perspective. Since this is easiest to understand in its consequences, let us discuss these matters from the perspective of the good old Bühlmann model.

I think it is indeed not controversial that smaller particles diffuse faster but that alone should make zero difference! This might sound surprising but let’s look at Bühlmann’s list of half-times (these are essentially inverses of the diffusion constants). Those are for nitrogen (in minutes):

const double buehlmann_N2_t_halflife[] = { 5.0, 8.0, 12.5, 18.5, 27.0, 38.3, 54.3, 77.0, 109.0, 146.0, 187.0, 239.0, 305.0, 390.0, 498.0, 635.0 };

const double buehlmann_He_t_halflife[] = { 1.88, 3.02, 4.72, 6.99, 10.21, 14.48, 20.53, 29.11, 41.20, 55.19, 70.69, 90.34, 115.29, 147.42, 188.24, 240.03 };

Obviously, there is a difference. But how did he measure those? The answer is: He didn’t. You can come up with those (starting from N2) only by theoretical reasoning. You assume that the relevant physics is diffusion. And that has only one parameter, the diffusion constant or half-time. And that you don’t know a priori. But you can imagine that you only need to look at processes at time scales compared to those encountered during a dive. And there, pressure changes at the order of a few minutes and the total dive length which is a few hours. So anything in between will be relevant. And this is what gives you those numbers! They vary from five minutes to 10.5 hours. Ideally you want to cover the whole range of in-between numbers but of course you can do this only for a finite number of values (here taken to be 16) which you then evenly spread in the interval. Where evenly means that consecutive ones differ by the same percentage (rather than absolute value), i.e. they form a geometric progression. And, guess what, they do.

Obviously, there is a bit of arbitrariness in this procedure, in particular in picking the smallest and the largest value and in the number of intermediate steps. But as long as the slowest or fastest compartment are not the leading compartment for a larger part of the deco and the gaps between adjacent tissue half-times are not too big, those choices should not really matter.

But this means that what seems to be the biggest difference between nitrogen and helium, the difference in half-times is really no difference at all! It only means, we parametrize the range of possible diffusion constants differently. Yes, compartment number four has a different half-time for N2 (18.5min) than for  He (7min) but there are compartments six and seven (half-times 14.48min and 20.53min) which would cover the same time range. (Note that thanks to the diffusion equation, the tissue loading after time is the Laplace transform of the ambient pressure and according to the structural similarity between Laplace and Fourier transform, the half-time plays the role of a frequency, so a tissue gets particularly excited if the ambient pressure changes at the same time scale which is like exciting on oscillator with its resonant frequency).

Keep in mind that “the tissue” does not really correspond to a certain part of the human body like muscles being modeled by compartment x and bones by compartment y (even though some layman’s explanations make you believe that), rather the range of tissues models the range of diffusion constants and our ignorance about the time constants that might play a role in a complex system like that of a diver during the dive.

So, if you did one dive in which the breathing mix contained a given fraction of nitrogen, then the tissue loading of compartment four would be the same as if the same profile would be dived with breathing a mix that contains that fraction now in helium and then in compartment six or seven (ignoring the fact that before the dive, at the surface you were breathing air and not heliox 79).

So much for tissue loadings (where the difference between N2 and He is only in a shift in compartment number). But what about M-values (parametrized by a- and b-coefficients in Bühlmann’s model)? Those are different for He and N2.

Yes, they are. When indexed by compartment numbers. But we just saw, those don’t mean much, we should rather look at them as a function of half-time. And then the difference is much smaller as can be seen by these diagrams:

Orange is helium, blue is nitrogen. There seems to be a systematic difference for slow tissues for a and for fast tissues for b but this goes essentially away once one plots the tolerated ambient pressure (the “M-value”) as a function of tissue loadin according to the linear equation

\(p_{tol}=(p_{i} – a) \times b\)
M-values for He and N2 as a function of tissue pressure and half-time

 

This plot shows \(p_{tol}\) as a function of (the log) of the half-time and the tissue loading and one sees there is hardly any difference between the orange and the blue surface (here is a version that you can rotate to look at it from all sides without coordinate frame though, thanks Mathematica). I computed all these plots in a Mathematica notebook that you can download here.

Again, the upshot is that once you align the tissue half-times, the difference between the two inert gases is quite small. So, why is there a “penalty” for using more helium in your mix (while there above mentioned study finds evidence for not so much difference)? Where does it come into the model?

The answer is that when actually diving trimix, that is having both N2 and He in your mix, one has to combine the effects of the two. In the Bühlmann model, you are supposed to add the partial tissue pressures and use the weighted average (weighted by the fractions of the two inert gases) of the M-values. And here it is, where you combine them using tissue number (and not as I did above) by half-time. The justification would be that due to the different diffusion rates this is what happens in a single tissue in the body (with the above mentioned caveat that these tissues are theoretical constructs of an interpolation and not necessarily reflect real physiological tissues).

The effect is that now some nitrogen load is compared to an M-value which partly comes from He which gives you a much stricter M-value (as the He-M-values are smaller when you compare them with aligned compartment number rather than half-time). This is where the penalty comes from.

To me it sounds as if it is this combining of the gases is actually the part of the Bühlmann model with the weakest justification from a physics point of view. And my interpretation of the NEDU study is that it supports doubts that this is the right thing to do.

It seems, further studies about this part, where one simply takes two gas compartments which happen to have the same compartment number (which is only a coordinate in diffusion constant space after all) and throws them together for the two different gases, are needed. At least, this is where I would put my money that this is an area where the models could be improved (or at least better empirically justified).

 

Update: In a previous version I had claimed that David Doolette had invented the heat-map display of decompression. It was pointed out to me that this was in fact user “UWSojourner” on several fora.