Author: robert

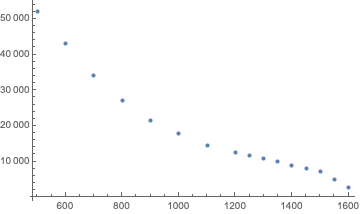
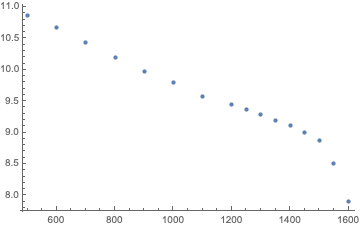
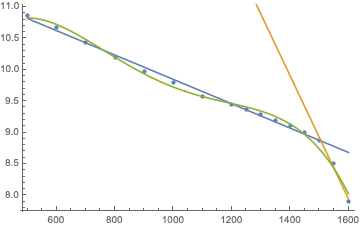
Here is another contribution by Doug Fraedrich. This time, the text would probably better fit on theepxerimentaldiver.org: He tests dive computers No-Fly-Times algorithms and compares those to DAN’s recommendations and the respective user manuals. For some more theoretical considerations regarding diving and flying, see this older post.

Introduction

It is well known that divers must wait a certain time after diving before then can safely fly. The current No Fly Time (NFT) “best practices” guidelines from Divers Alert Network (DAN)¹ are listed below:

• For a single no-decompression dive, a minimum preflight surface interval of 12 hours is suggested. 
• For multiple dives per day or multiple days of diving, a minimum preflight surface interval of 18 hours is suggested. 
• For dives requiring decompression stops, there is little evidence on which to base a recommendation and a preflight surface interval substantially longer than 18 hours appears prudent

These guidelines are primarily based on a paper by Richard D. Vann, et al² of Divers Alert Network, which reported an analysis of risk of Decompression Sickness (DCS) results of 802 dives of nine different profiles: four single non-deco dives and five sets of repetitive dives. DAN did not test decompression dives in Reference 2, so the US Navy No Fly Times were used for this category of dives.

Many commercial off-the-shelf dive computers compute and display this time after surfacing from a dive. The level of documentation on how exactly this is computed varies from dive computer to dive computer; most units state in their manual that they use the DAN guidelines.

The objective of this report is to test several representative commercial off-the-shelf dive computers in pressure chamber which simulates different categories of dives and assess the following: 1) does each computer conform to the DAN NFT guidelines? and 2) does each computer conform to what is described in the computer’s owner’s manual? The dive computers tested are shown in Figure 1 and listed in Table 1. 

Methods

The dive computers were subjected to simulated dives in a small pressure chamber, Figure 2. This chamber was a Pentair Pentek Big Blue 25cm chamber that had a maximum allowable pressure of 6.9 bar. 

The units-under-test are placed in the chamber with the display facing out (as illustrated in Figure 2) and filled with fresh tap water. Air pressure is added from the top of the chamber via a standard bicycle pump (Velowurks Element floor pump.) Even though the relationship between pressure and indicated depth is well-known, several “calibration runs” were performed before the testing to verify repeatabilty of calibration. For these calibration runs, a Shearwater Perdix dive computer was used.

Pressure was released in a controllable way via an added vent valve. This ensured that the simulated ascent rates were not too fast. Figure 3. 

Figure 4 shows an actual profile using the test chamber.

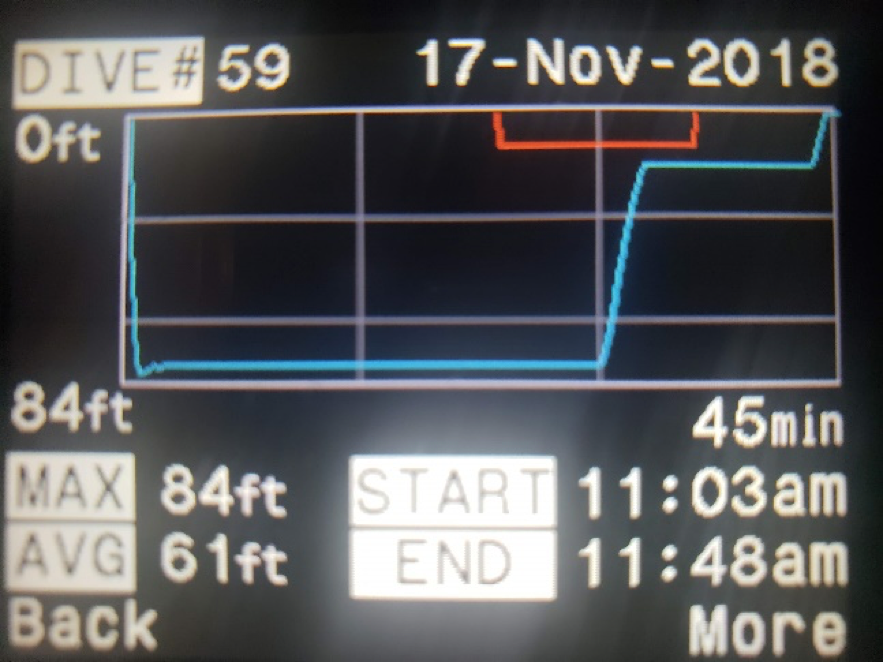
A run list was prepared based on the dives described in Reference 2; see run list in Table 2.

Some of the dive times needed to be shortened, compared to the original dives in Reference 2; this is because the bottom times in the “old” no-deco dives exceeded the No Decompression Limits on some of the computers tested.  Since decompression dives were not tested in the DAN study in Reference 2, two dives profiles were added to the test matrix:  a “marginal” deco dive, profile #10 (US Navy Repetitive group H) and a deeper, more stressing deco dive, Profile 14 (US Navy Repetitive Group L).³   US Navy recommended No Fly Times are listed in the table. The specific bottom time for the marginal deco dive was chosen by what was required to make the most conservative of all the computers go into decompression mode.  The last category of “Violation Dives” was added to test claims made in some of the manufacture’s User Manuals.  The dive profiles in Table 2 were simulated and the displayed No Fly Time from each computer was recorded. The battery charge level was monitored for each computer and kept at acceptable levels. With the exception of the repetitive dives with a 1 hour surface interval, the interval between consecutive runs was the maximum of: 24 hours, desaturation time and the longest displayed NFT from any computer.

Results

A total of 26 runs were performed in this study; the raw results are shown in Table A1 in the Appendix.  To start off the testing,  Profile #2  was replicated several times to assess that the results were repeatable. For all of the runs, the water temperature varied from17C to 23C; when repetitive dives were simulated, the water was not completely replenished with new tap water, so the second (and third) dives of repetitive sequences tended to have a water temperature about 1-2 C warmer than the first. The ascent rate was monitored using several different dive computers, but the SEAC Guru displayed numerical values with units of ft/min; ascent rates were constantly monitored and were typically in the range of 5-15ft/min (1.5 -5 m/min). 

The results from Appendix A1 are summarized in Table 3. Based on this data, each of the eight dive computers can be assessed as to whether they are compliant with the DAN guidelines and if they actually compute what is described in their manuals. 

Discussion

Single Dives:

All of the computers were compliant with the DAN guidelines for this type of dive.  It was observed that both Mares and Suunto increased their NFT after the exact same single dive profile (#2) separated by a surface interval of ~ 44 hours. There is little documentation on the Mares RGBM variant, but the Sunnto variants are known to factor in the effects of multi-day diving in bubble growth (and presumably desaturation) calculations. This multi-day factor, known as “F3”, persists for up to 100 hours⁴, Figure 4. Multi-day diving is not covered in the DAN NFT guidelines.

Repetitive Dives:

All of the computers were compliant with the DAN guidelines for this type of dive.  For the Suunto EON Steel, since this computer based Repetitive NFT on desaturation times, the reported NFT depended on the exact nature of the repetitive dives and presumably the dives in the previous 100 hours.

Decompression Dives:

Two computers registered an NFT of less than 18 hours for the Group H deco dive: Deepblu Cosmiq+  required only 12 hours of NFT, and the Suunto EON Steel required a range of NFT from 17:35 to 21:18, (depending on previous dives and surface interval.) Note that in both User Manuals, they stated that NFT’s were based on internally-computed De-Sat times and not the DAN guidelines.  The Group L dive required significant total decompression time (~60 mins): all of the computers registered the same NFT as the Group H dive, except the Suunto EON Steel which increased the required NFT to 26:13 which is above the DAN guideline.   It should be noted that all computers registered NFT’s that exceeded that suggested by the US Navy for Repetitive group H³, however the Deepblue Cosmiq+ would fall short of the US Navy recommendation if used for deco dive having repetitive group I or more.

Violation Dives:

Some computers mentioned in their User Manual that they added an extra NFT penalty for ascent rate violations. Different computers defined “fast ascent violation” differently, so a target ascent rate of 50ft/min was used in Profile #13, which qualified as a fast ascent for all computers. Profile #13 was executed and the actual ascent rate varied from 9-15 m/min during the ascent from 18 to 5m, which took about one minute. A three minute safety stop at 5m was performed. None of the computers seemed to adjust the NFT, based on a comparison to similar dives with a nominal ascent rate, Profiles 2, 6a, 7a, 9a. Alarms did go off during the fast ascent from several computers. The Safety Stop may have been sufficient to satisfy all of each computers’ Dive Algorithms’ safety requirements. Similarly, none of the computers added an extra NFT penalty for dive Profile #11, which was a no-deco dive, with nominal ascent rate but missed safety stop.

For omitted stops on a deco dive (Run # 20, Profile 12), four computers added additional NFT time, compared to the same profile deco dives with all the required stops (Run # 17 profile 10.) See Table 4.

User Manual Discrepancies:

It was noted that several computers did not conform with the NFT rules stated in their User Manual; see Table 5.

Summary

Eight commercial dive computers were tested in a small pressure chamber to assess their computation and display of No Fly Times. All of the dive computers were found to be generally compliant with the standard DAN guidelines with a few exceptions. Several computers used a very simple rule for NFT: Garmin, Aqualung, Oceanic and Cressi simply displayed 24 hours NFT for all nominal dives (both no-deco and decompression).  Some computers added features that handled cases not covered in the DAN guidelines, e.g. multi-day diving (Mares and Suunto) and certain decompression guidance violations such as omitted decompression stops (Garmin, Suunto, Cressi and DeepBlu).

References

1. https://www.diversalertnetwork.org/medical/faq/Flying_After_Diving
2. Richard D. Vann, et al “Experimental trials to assess the risks of decompression sickness in flying after diving”  Journal of Undersea and Hyperbaric Medicine, 2004
3. US Navy Diving Manual, Version 7, 2016, Tables 9-7 and 9-6.
4. Suunto Reduced Gradient Bubble Model. June 2003. Available from: http://www.dive-tech.co.uk/resources/suunto-rgbm.pdf. [cited 2017 August 29].

Appendix A. Raw Test Results by Run

You wouldn’t be here if you didn’t enjoy quantitative analysis of anything diving. There is a special treat for you: Thanks mainly to Willem and Berthold of the Subsurface development team, you can now use Subsurface to do all kinds of statistics on you dive log. There are many cool graphical representations of looking at essentially any variable from your log (depth, duration, date, SAC, rating, visibility, gas use, oxygen or helium percentage, location, buddy etc etc) as functions of each other:

Go ahead and see how your SAC changes over time or which buddy you do the longest dives with or if you use less gas on dives with better visibility.

This is still an an alpha testing phase and crashes are still possible and things will change before the next upcoming release. But you can download a test version from our daily builds. There are also mobile version available from Testflight for iOS and the Google PlaysStore beta program. Please comment on the Subsurface mailing list or on Github if you find bugs or have ideas for improvement.

I was thinking what might be a good measure for decompression quality or stress. This also comes as O’Dive with their end user Doppler Device claim to provide exactly that in their mobile phone application. As said before, I have some doubts about their approach, so let’s try to come up with something better.

As always here on TheTheoreticalDiver, everything is entirely theoretical, I have zero empirical data of my own. But with this disclaimer, here we go:

I think we all agree on the fact that decompression stress comes arises as tissue pressure exceeds ambient pressure and that also the time of this excess pressure is relevant.

But measuring the excess pressure in mbar is probably not very useful as this is not a natural measure of decompression stress (and the relation might as well depend on the tissue under consideration as well as ambient pressure and a million other things). The gradient factor approach is to normalise this excess pressure with the maximally allowed excess pressure (which is the definition of the gradient factor) and this sounds like a good start.

But rather than comparing to plain vanilla 100/100 Bühlmann, I would like to be more flexible and compare to your decompression model of choice. So I would like to take

as a measure of momentary stress where p_i,max is the maximal allowed inert gas pressure in tissue number i as given by your decompression model.

This could be plain Bühlmann in which case this expression is just your momentary gradient factor. Or you believe in excess pressure being worse at depth (as the produced bubbles will grow later on in shallower water) then you take p_i,max as given by Bühlmann corrected by your favourite settings of GF_low and GF_high. Or you insist on using VPM-B then you use the maximal momentary M-value as predicted by that model. Strictly speaking this is an extension of that model for real (as opposed to planned) dives, but at least in Subsurface, we have found a way to compute it (such that it pretty much agrees on planned dives).

Obviously, if you decompress exactly as prescribed by you model, q=1 during decompression (possibly a bit lower due to the fact that most people decompress in steps of 10ft/3m rather than continuously). But

is the definition of not violating the ceiling.

The ceiling being what it is, violating it should be bad and the more the worse whereas staying way below the ceiling gives your additional conservatism which you probably have to pay in terms of extended decompression time.

So, my proposal would be to compute the L^lambda norm of the function q(t) for somewhat large lambda as this punishes going above q=1:

To me, this seems to be a reasonable measure of deco stress. Maybe it’s worthwhile to compute this for a number of real profiles and compare it deco outcome (risk of DCS, I wish I had access to the DAN data… or at least Doppler results).

What do you think?

In a recent article in GUE’s InDepth blog, Richard Walker argues that the correct unit to discuss the amount of (free) gas in a cylinder is l (litre) and not bar l (bar times litre) because that is the correct unit for a volume.

I would like to argue that although the latter is correct the former isn’t: The volume of the gas is not its amount. The amount is measured by counting the number of molecules or (if you don’t like big numbers) the number of moles of gas. Let’s look at the ideal gas law, the mother of all gas calculations (and of course including Boyle-Mariotte):

It’s the n on the right hand side (or nR depending on whether you count molecules or moles). As during diving, the temperature stays pretty much constant (or at least we don’t take changes in to account in our calculations) you could include that in the constant as well. Then the RHS (and thus the LHS) describes the diver’s version of amount of gas.

And that is not changed even when feeding it though a compressor (let’s still ignore the temperature change), when emptying the cylinder at the surface or when breathing it at 30m of depth at ambient pressure. This is the amount.

And you should measure it in the unit of this equation which is volume times pressure, which in SI derived unites is conveniently expressed in bar l.

Of course you can compute which volume this amount of gas fills at some pressure (be it 232 bar or 1 bar or 4 bar in the above examples), simply divide by that pressure. But when gas planning, you should plan the amount of gas you need (you will need it at different pressures) and that is measured (invariantly) in bar l.

I am sorry Rich, but I believe you are wrong here.

Nothing profound to say these days (in which I guess more people practice the theoretical side of diving). But yesterday, I was watching the first few episodes of season 3 of Money Heist (La casa de Papel, Haus des Geldes) on Netflix. And not only the professor is complaining that he had too little time to work out the plan, it seems this also applies to the script writers.

I am willing to forgive questionable approaches to tracking satellite phones and hacking into mobile phones. But when it comes to theoretical diving, there is a limit!!1!

I don’t want to spoiler too much, let’s just say, there is a flooded vault and they are diving to extract bars of gold:

Wasn’t anybody aware that the density of gold is almost twice the density of lead? A good delivery bar weights 12,4 kg, so the woman holding two of whose on stretched out arms has spent a lot of time in the gym. Also, swimming two of those to the exit it will be challenging to maintain neutral buoyancy…

When I was a student at DESY (the German particle accelerator lab in Hamburg), even in the theory building, we used lead blocks the size of half bricks as door stops, monitor mounts etc. Those came from the experimentalists who used those as means of radiation protection. The first time, you tried to pick up one of those, you got the impression it was screwed to the floor as your brain expected to pick up something they weight of a brick. But no, the density of concrete is about twice that of water while lead is about 11 kg per litre while gold is 19 kg per liter.

Over at GUE’s InDepth blog, Jarrod Jablonski has published a first post in an upcoming series on past and future of decompression protocols. A definite must-read, not only because it’s one of the leaders of the industry laying out his point of view.

The part I find most interesting for future developments is the research into exercise about before diving to reduce the number of micro bubbles from the blood and the idea to even to replace that with giving nitric oxide (NO) or substances that lead to the release of NO (like Viagra) prior to diving could cut short decompression times. This is probably far too early to know but I remember recently seeing a report of a cave dive on Facebook that mentioned some medicine was taken before the dive to shorten decompression without giving any details. Unfortunately, I cannot find the link anymore, maybe one of my readers can supply it.

But I think this would be the right time to think through a possible scenario: Assume research shows that there is a substance X that divers can take before big dives that would significantly shorten decompression while still maintaining the same level of safety. But substance X has long term side effects (NO has a toxic dose and is chemically related to NO2 which is a the heart of the Diesel engine scandal). Would we then see this as the diver’s analogue of doping? Could this lead to a situation similar to body building and steroids? There would be a general advice not to use such substances because of their side effects but maybe at that time, for the next big dives, decompression obligations would be so big that explorers could justify the short term benefits over the long term risks. But for every explorer there are orders of magnitude more followers who are going to imitate their heroes and thus would also start using such drugs although in their case there is no good justification. Just because they want to do everything like the people they look up to (not that would happen anywhere in the tech diving community…).

I would say now would be a good time to come up with an opinion on how such a situation were to be handled, what are the limits of what one could and should ethically do. Of course, everything would have to be adjusted once the actual thing with all details are known. But it wouldn’t hurt to come up with a basic opinion whilst all this is still theoretical.

Note: I originally meant this to be a comment under the InDepth blog post but I did not manage to create and account there that would allow me to post it. Does anybody know how (i.e. where) I could do that?

Update: The InDepth website now allows me to post.